Question

an airplane is heading north at an airspeed of 600 km/hr, but there is a wind blowing from the southeast at 40 km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?

Answer 1

To determine how many degrees off course the airplane will end up flying and its speed relative to the ground due to the wind, we can use vector addition.

Step 1: Set up the problem.

Let's represent the airplane's airspeed vector as
`A` and the wind's velocity vector as
`W`

A points north and has a magnitude of 600 km/hr.

W points from the southeast. This means it has components blowing to the west and to the north.

Since southeast is midway between south and east, the wind's direction can be split into two perpendicular components (north and west) of equal magnitude. The magnitude of each component is:

`(40)/(\sqrt2)`

​

​

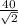
Step 2: Determine the components of the wind vector

Northward component
`W_N` = 
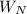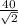`(40)/(\sqrt2)` = 28.28 km/hr

Westward component
`W_W` =
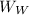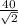`(40)/(\sqrt2)` = 28.28 km/hr

Step 3: Determine the resultant velocity of the airplane relative to the ground

Northward component
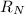`R_N` = Airplane's northward velocity + Wind's northward velocity = 600 km/hr + 28.28 km/hr = 628.28 km/hr

Westward component
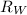`R_W` = 28.28 km/hr ( since the airplanes westward velocity without wind is 0)

Step 4: Calculate the magnitude and direction of R using the Pythagorean theorem and trigonometry.

Magnitude:

`R= √((R_N)^2+(R_W)^2)`

`R=√((628.28)^2+(28.28)^2)`

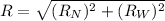
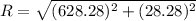
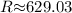`R$\approx$629.03` km/hr

Direction

Using the tangent function

`Tan(\theta) = (opposite)/(adjacent) = (R_W)/(R_N)`

`\Theta = tan^-1((28.28)/(628.28))`

`\theta$\approx$2.57^\circ`

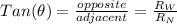
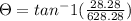
So, the airplane will end up flying approximately 2.57° west of north, and its speed relative to the ground is approximately 629.03 km/hr.