Question

Four of the interior angles of a pentagon are each equal to 104°.
Calculate the fifth angle.

Answer 1

Explanation:

Interior angles of a n-gon sum = ( n-2) * 180 degrees

for a pentagon : sum = ( 5-2) * 180 = 540 degrees

540 - 4 *104 = 5th angle = 124 degrees

Answer 2

Fifth interior = 124°

Explanation:

The sum of the interior angles in a polygon with n sides is given by the formula:

`\sf \textsf{Sum of interior angles = }(n - 2) * 180^\circ.`

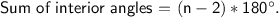
For a pentagon (a polygon with 5 sides), the sum of its interior angles is:

`\sf \textsf{Sum of interior angles =} (5 - 2) * 180^\circ= 3 * 180^\circ= 540^\circ`

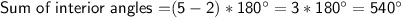
Given that:
Four of the interior angles of the pentagon are each equal to 104°, you can find the fifth angle by subtracting the sum of the four known angles from the sum of the interior angles of the pentagon:

`\boxed{\textsf{Fifth angle = Sum of interior angles - Sum of four known angles}}`

`\sf Fifth angle = 540^\circ - (4 * 104^\circ ) = 540^\circ - 416^\circ = 124^\circ`

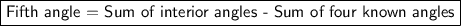
Therefore, the fifth interior angle of the pentagon measures 124°.