The radius of convergence
 for the original series
for the original series
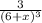 is
is
 .
.
The power series expansion of the function
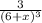 up to six terms is given by:
up to six terms is given by:
![\[(1)/(72) - (x)/(144) + (x^2)/(432) - (5x^3)/(7776) + (5x^4)/(31104) - (7x^5)/(186624) + \cdots\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qmugn5i7skqs4ysenhllme6olx12mgznse.png)
Now, let's find the radius of convergence
 for this series.
for this series.
The general term of the binomial series
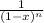 is given by
is given by
 , where
, where
 is the binomial coefficient. In our case, for
is the binomial coefficient. In our case, for
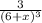 , we can rewrite the function as
, we can rewrite the function as
 and apply the binomial series expansion with
and apply the binomial series expansion with
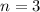 and
and
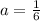 .
.
The radius of convergence of the binomial series
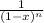 is 1, so for our transformed series, the radius of convergence will be
is 1, so for our transformed series, the radius of convergence will be
 .
.
Therefore, the answer is
 .
.
The complete question is here:
Use the binomial series to expand the function as a power series.
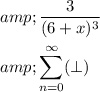 (______)
(______)
State the radius of convergence,
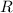 .
.