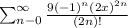Question

Use a Maclaurin series in this table to obtain the Maclaurin series for the given function. :

f(x) =9sin ^2 (x) [Hint: use sin^2(x) 1/2(1-cos(2x)]

Answer 1

The Maclaurin series for
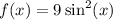`f(x)=9 \sin ^2(x)` is given by
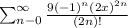`\sum_(n-0)^(\infty) (9(-1)^n(2 x)^(2 n))/((2 n) !)` . This series represents the expansion of
`9 \sin ^2(x)` around the point x=0 using the derivatives of the function at that point. The series includes terms for all non-negative integer values of n. The general term in the series is
`(9(-1)^n(2 x)^(2 n))/((2 n) !)`

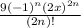
The Maclaurin series expansion for
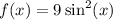`f(x)=9 \sin ^2(x)` can be obtained by substituting the given hint into the function. The Maclaurin series for
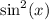`\sin ^2(x)` can be expressed using the hint as follows:

`\sin ^2(x)=(1)/(2)(1-\cos (2 x))`

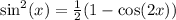
Now, substitute this into the original function
`f(x)=9 \sin ^2(x)` :

`f(x)=9 \cdot (1)/(2)(1-\cos (2 x))=(9)/(2)(1-\cos (2 x))`

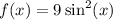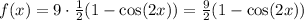
Now, let's express cos(2x) as a Maclaurin series. The Maclaurin series for cos(x) is well-known:

`\cos (x)=\sum_(n=0)^(\infty) ((-1)^n)/((2 n) !) x^(2 n)`

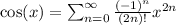
So, for cos(2x):

`\cos (2 x)=\sum_(n-0)^(\infty) ((-1)^n)/((2 n) !)(2 x)^(2 n)`

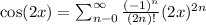
Now, substitute this into the expression for f(x):

`f(x)=(9)/(2)\left(1-\sum_(n-0)^(\infty) ((-1)^n)/((2 n) !)(2 x)^(2 n)\right)`

To obtain the Maclaurin series for f(x), you can distribute the 9/2 and simplify the expression:

`f(x)=(9)/(2)-(9)/(2) \sum_(n-0)^(\infty) ((-1)^n)/((2 n) !)(2 x)^(2 n)`

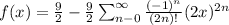
So, the Maclaurin series for
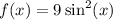`f(x)=9 \sin ^2(x)` is
`\sum_(n-0)^(\infty) (9(-1)^n(2 x)^(2 n))/((2 n) !)`