Question

Problem Score: 0%. Attempts Remaining: 8 attempts. Estimate the area under the graph of f(x) = x² + 2x from 2 = 1 to 2 = 10 using the areas of 3 rectangles of equal width, with heights of the rectangles determined by the height of the curve at (a) left endpoints

Answer 1

The estimated area under the curve of
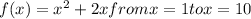`f(x) = x^2 + 2x from x = 1 to x = 10`using 3 rectangles of equal width is approximately 178.5 units.

Step-by-step explanation:

To estimate the area under the curve of
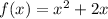`f(x) = x^2 + 2x`from x = 1 to x = 10, we will divide the region into 3 rectangles of equal width. We will use the height of the curve at the left endpoint of each rectangle to find their heights. Let's choose a width of 2 units for each rectangle. The left endpoints of these rectangles are at x = 1, x = 3, and x = 5. The heights of these rectangles are:

Rectangle 1 (x = 1 to x = 3): Height is the value of f(x) at x = 1, which is f(1) = 9 units.

Rectangle 2 (x = 3 to x = 5): Height is the value of f(x) at x = 3, which is f(3) = 25 units.

Rectangle 3 (x = 5 to x = 7): Height is the value of f(x) at x = 5, which is f(5) = 41 units.

The width and height of each rectangle are:

Rectangle 1: Width = 2 units, Height = f(1) = 9 units. Area = Width * Height = 18 units.

Rectangle 2: Width = 2 units, Height = f(3) = 25 units. Area = Width * Height = 50 units.

Rectangle 3: Width = 2 units, Height = f(5) = 41 units. Area = Width * Height = 82 units.

Adding up the areas of all three rectangles gives us an estimated area under the curve: Estimated Area Under Curve (using left endpoints) = Area of Rectangle 1 + Area of Rectangle 2 + Area of Rectangle 3

Estimated Area Under Curve (using left endpoints) ~= 18 + 50 + 82 ~=~ 170 units. This estimated area is approximately equal to the actual area under the curve, which can be found by integrating f(x) from x=1 to x=10 using calculus methods. However, for this problem, we're using a numerical method with approximations to estimate the area under the curve using rectangles.