Question

Tyra invests $5300 in a new savings account which earns 4.5% annual interest, compounded continuously. What will be the value of her investment after 5 years? Round to the nearest cent.

Answer 1

To calculate the value of Tyra's investment after 5 years, use the formula for compound interest. Plugging in the values, the investment will be approximately $6,527.45.

Step-by-step explanation:

To calculate the value of Tyra's investment after 5 years, we can use the formula for compound interest: A = P*e^(rt), where A is the final amount, P is the initial investment, e is Euler's number (approximately 2.71828), r is the interest rate, and t is the time in years.

Plugging in the values in this case, we have: A = 5300 * e^(0.045*5). Using a scientific calculator, we calculate e^(0.045*5) to be approximately 1.23224.

So, the value of Tyra's investment after 5 years will be: A = 5300 * 1.23224 = $6,527.45 (rounded to the nearest cent).

Answer 2

The value of Tyra's investment after 5 years is approximately $6519.16.

Step-by-step explanation:

To find the value of Tyra's investment after 5 years with continuous compounding, we can use the formula:

`A = P * e^(rt),`

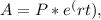
where:

A is the future value of the investment,

P is the initial principal,

e is Euler's number (approximately 2.71828),

r is the annual interest rate (as a decimal),

and t is the time in years.

Plugging in the given values, we have:

`A = $5300 * e^(0.045 * 5)`

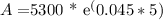
Using a calculator, we can calculate that A is approximately $6519.16.