Question

Exponential growth and decay problems follow the model given by the equation A(t)=Pe rt

. - The model is a function of time t - A(t) is the amount we have after time t - P is the initial amount, because for t=0, notice how A(0)=Pe 0.t
=Pe 0
=P - r is the growth or decay rate. It is positive for growth and negative for decay Growth and decay problems can deal with money (interest compounded continuously), bacteria growth, radioactive population growth etc. So A(t) can represent any of these depending on the problem. Practice The growth of a certain bacteria population can be modeled by the function A(t)=400e 0.0509t
where A(t) is the number of bacteria and t represeno the time in minutes. a. What is the initial number of bacteria? (round to the nearest whole number of bacteria.) b. What is the number of bacteria after 15 minutesi (round to the nearest whole number of bacteria.) c. How long will it take for the number of bacteria to double? (your answer must be accurare

Answer 1

The initial number of bacteria is 400. After 15 minutes, the number of bacteria grows to approximately 895. It would take about 13.61 minutes for the bacteria population to double.

Step-by-step explanation:

The student's question revolves around an exponential growth function that models the growth of a bacteria population over time. The formula provided is A(t) = 400e0.0509t, where A(t) represents the number of bacteria at time t, e is the base of the natural logarithm, and 0.0509 is the growth rate.

a. The initial number of bacteria, which is when t = 0, is found by substituting 0 into the formula, yielding A(0) = 400e0 = 400. Therefore, the initial number of bacteria is 400.

b. To find the number of bacteria after 15 minutes, we substitute t = 15 into the formula: A(15) = 400e(0.0509×15). This calculation results in A(15) being approximately 895.48, which rounds to the nearest whole number as 895 bacteria.

c. To calculate the time it would take for the number of bacteria to double, we need to solve for t when A(t) is twice the initial amount, that is 2×400 = 800. We use the formula 800 = 400e0.0509t. Dividing both sides by 400 gives us 2 = e0.0509t, and taking the natural logarithm of both sides lets us solve for t, which is approximately 13.61 minutes.

Answer 2

The student's question requires understanding and applying the exponential growth model
`A(t)=Pe^{rt` to a bacteria growth problem, including finding the initial population, the population after a set time, and the time required for the population to double.

Step-by-step explanation:

The question pertains to exponential growth, which is a crucial concept in various scientific fields, including biology and finance. Exponential growth occurs when a quantity increases at a rate proportional to its current value, such as populations or investments that grow continuously over time. The student's question involves using the mathematical model
`A(t)=Pe^(rt)` to solve problems about bacteria growth.

Initial Number of Bacteria

To find the initial number of bacteria, we look at the equation
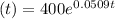`(t) = 400e^{0.0509t` and observe that when t is 0, the initial amount P is thus A(0) = 400. This represents the population of bacteria at t = 0.

Number of Bacteria After 15 Minutes

After 15 minutes, to find the number of bacteria, we substitute t with 15 in the equation, resulting in
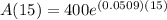`A(15) = 400e^{(0.0509)(15)`. Calculating this value will give us the number of bacteria after 15 minutes, rounded to the nearest whole number.

Time for Bacteria to Double

For the population to double, we need to find the time t where A(t) is equal to twice the initial population:
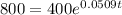`800 = 400e^{0.0509t`. Solving this equation for t will give us the time required for the bacteria population to double.