Question

Find the point on the plane x − 2y + 3z = 9 that is closest to the point (0, 1, 2)

Answer 1

To find the point on the plane x - 2y + 3z = 9 that is closest to the point (0, 1, 2), we use the distance formula and the equation of the plane to find the coordinates of the closest point.

Step-by-step explanation:

To find the point on the plane x - 2y + 3z = 9 that is closest to the point (0, 1, 2), we first find the distance between the given point and any arbitrary point on the plane using the distance formula. Let's assume a point (x, y, z) on the plane. The distance between the two points can be calculated as:

distance = sqrt((x - 0)^2 + (y - 1)^2 + (z - 2)^2)

Next, we substitute the equation of the plane x - 2y + 3z = 9 into the distance formula and minimize the distance by differentiating it with respect to x, y, and z, and setting the derivatives equal to zero. Solving these equations will give us the coordinates of the point on the plane that is closest to the given point.

Answer 2

To find the point on the plane x - 2y + 3z = 9 that is closest to the point (0, 1, 2), calculate the perpendicular distance between the plane and the point using the formula for the distance between a point and a plane. The calculated distance is approximately 2.267 units.

Step-by-step explanation:

To find the point on the plane that is closest to the point (0, 1, 2), we need to find the perpendicular distance between the plane and the point. This distance can be calculated using the formula for the distance between a point and a plane. Given the equation of the plane as x - 2y + 3z = 9, the unit normal vector to the plane is (1, -2, 3).

We can use the formula:

Distance =
`|(ax0 + by0 + cz0 + d)| / \sqrt(a^2 + b^2 + c^2),`

where (a, b, c) is the normal vector to the plane, and (x0, y0, z0) is the coordinates of the point.

Substituting the values into the formula:

Distance =
`|(1)(0) + (-2)(1) + (3)(2) + (-9)| / \sqrt{1^2 + (-2)^2 + 3^2)`

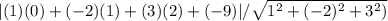
= |4| / √14

= 2.267.