Question

A wrecking ball used to knock down buildings has a mass of m = 1140 kg and is suspended from a cable of length L = 17 m. It reaches a maximum speed of v = 19 m/s while traveling in a circular arc toward the building.

A) What is the minimum tension in N that the cable must be able to support without breaking? Assume the cable is massless.
B) If the cable can only support a tension of 10,000 N what is the highest mass the ball can have in kg?

Answer 1

The minimum tension in the wrecking ball's cable is approximately 21,958 N, and the highest mass the ball can have without breaking a cable that supports 10,000 N of tension is around 735 kg.

Step-by-step explanation:

To address the given problem, we first need to consider the forces acting on the wrecking ball as it swings towards the building. The tension in the cable, when the ball reaches its maximum speed, will be a combination of the force due to gravity (weight of the ball) and the centripetal force required to keep the ball moving in a circular path.

A) To find the minimum tension in the cable (T), we can use the following formula which combines the weight (mg) and the centripetal force (
`mv^2/L`):
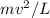T = mg +
`mv^2`/L.
Plugging in the given values (m = 1140 kg, g = 9.81 m/s2, v = 19 m/s, L = 17 m), we get:
T = 1140 kg × 9.81
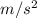`m/s^2` + (1140 kg × 19
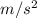`m/s^2`) / 17 m ≈ 21,958 N.

B) To find the maximum mass the ball can have without exceeding a cable tension of 10,000 N, we set T to 10,000 N and solve for m:
10,000 N = m × 9.81
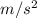`m/s^2` + (m × 19
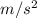`m/s^2`)/17 m;
after solving for m we get ≈ 735 kg.