Question

SUM 1 PLEASE HELP I GOT THE FIRST ONE BUT NEED HELP ON THE OTHERS

Answer 1

(a)

1. 10

2. 1/9

3. 1/16

(b)

1. 1/18

2. 1

Explanation:

Part (a): To rewrite the given fractions using factors and exponents, we can express both the numerator and the denominator as exponents. Then we will utilize the properties of exponents. This will help us simplify the fractions more easily.

1. 1000/100:

Numerator:

`\rightarrow 1000 = 100 * 10 = 10 * 10 * 10 = \boxed{10^3}`

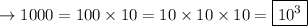
Denominator:

`\rightarrow 100 = 10 * 10 = \boxed{10^2}`

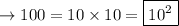
Thus, we have:

`\Longrightarrow (10^3)/(10^2)`

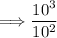
Use the third exponent property to simplify:

`\Longrightarrow (10^3)/(10^2) = 10^(3-2)=10^1=\boxed{10}}\\\\\\\\\therefore \boxed{\boxed{(1000)/(100)=10 }}`

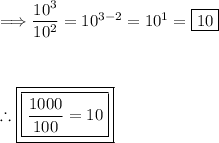
2. 9/81:

Numerator:

`\rightarrow 9 = 3 * 3 = \boxed{3^2}`

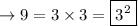
Denominator:

`\rightarrow 81 = 9 * 9 = 3 * 3 * 3 * 3 = \boxed{3^4}`

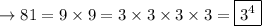
Thus, we have:

`\Longrightarrow (3^2)/(3^4)`

Use the third exponent property:

`\Longrightarrow (3^2)/(3^4)=3^(2-4)= \boxed{3^(-2)}`

Use the seventh exponent property:

`\Longrightarrow 3^(-2)=\boxed{(1)/(3^2)}`

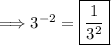
Lastly, evaluate the expression:

`\Longrightarrow (1)/(3^2)=(1)/(3 * 3)=\boxed{(1)/(9) }\\\\\\\\\therefore \boxed{\boxed{(9)/(81) = (1)/(9) }}`

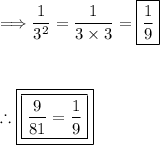
3. 4/64:

Numerator:

`\rightarrow 4 = 2 * 2 = \boxed{2^2}`

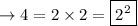
Denominator:

`\rightarrow 64 = 8 * 8 = 4 * 2* 4 * 2 = 2* 2 * 2 * 2 * 2 * 2 = \boxed{2^6}`

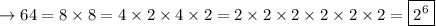
Thus, we have:

`\Longrightarrow (2^2)/(2^6)`

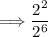
Use the third exponent property:

`\Longrightarrow (2^2)/(2^6)= 2^(2-6)=\boxed{2^(-4)}`

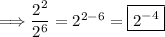
Use the seventh exponent property:

`2^(-4)= \boxed{(1)/(2^4)}`

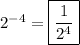
Lastly, evaluate the expression:

`\Longrightarrow (1)/(2^4)=(1)/(2*2*2*2)= (1)/(4*4)=\boxed{(1)/(16)}\\\\\\\\\therefore \boxed{\boxed{(4)/(64)=(1)/(16) }}`

`\hrulefill`

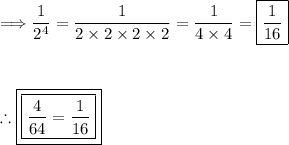
Part (b): To simplify the given expressions, we will utilize the properties of exponents.

1.

Given:

`((3 * 3))/((6 * 6 * 6)) * ((6 * 6))/((3 * 3 * 3))`

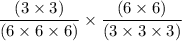
Simplifying the numerator and denominator into their exponents:

`\Longrightarrow ((3 * 3))/((6 * 6 * 6)) * ((6 * 6))/((3 * 3 * 3)) = \boxed{(3^2)/(6^3) * (6^2)/(3^3)}`

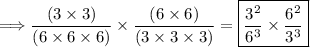
Apply the third exponent property:

`\Longrightarrow (3^2)/(6^3) * (6^2)/(3^3) = (3^2*6^2)/(3^3*6^3) = 3^(2-3) * 6^(2-3)= \boxed{3^(-1) * 6^(-1)}`

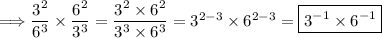
Apply the seventh exponent property:

`\Longrightarrow 3^(-1) * 6^(-1) = (1)/(3^1) * (1)/(6^1) * = \boxed{(1)/(3) * (1)/(6) }`

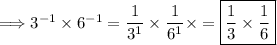
Evaluate the expression:

`\Longrightarrow (1)/(3) * (1)/(6) = (1)/(3*6) = \boxed{(1)/(18)}\\\\\\\\\therefore \boxed{\boxed{((3 * 3))/((6 * 6 * 6)) * ((6 * 6))/((3 * 3 * 3))=(1)/(18) }}`

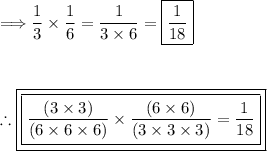
2.

Given:

`\Big((2^3)/(2^5) \Big)/\Big((2^0)/(2^2) \Big)`

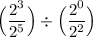
Apply the third exponent property:

`\Longrightarrow \Big((2^3)/(2^5) \Big)/\Big((2^0)/(2^2) \Big) = (2^(3-5)) /(2^(0-2))= \boxed{2^(-2) /2^(-2)}`

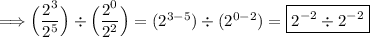
Apply the third exponent property again:

`\Longrightarrow 2^(-2) /2^(-2) = 2^(-2-(-2))=2^(-2+2) = \boxed{2^0}`

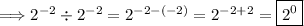
Apply the first exponent property:

`\Longrightarrow 2^(0)= \boxed{1}\\\\\\\\\therefore \boxed{\boxed{\Big((2^3)/(2^5) \Big)/\Big((2^0)/(2^2) \Big)=1}}`

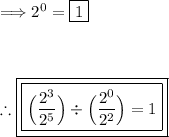
Thus, all given parts have been solved.

`\hrulefill`

Additional information:

Properties of Exponents: The properties of exponents are a set of rules that govern the manipulation and simplification of expressions involving exponential notation. They are given as follows:

`\boxed{\left\begin{array}{ccc}\text{\underline{Properties of Exponents:}}\\\\1.\ a^0=1\\\\2.\ a^m * a^n=a^(m+n)\\\\3.\ a^m / a^n \ ((a^m)/(a^n) )=a^(m-n)\\\\4.\ (ab)^m=a^mb^m\\\\5.\ (a/b)^m=a^m/b^m\\\\6.\ (a^m)^n=a^(mn)\\\\7.\ a^(-m)=1/a^m\\\\8.\ a^(m/n)=(\sqrt[n]{a} )^m\end{array}\right}`