Question

The graph of the equation x^2 = 4py is a parabola with focus F(x, y) = ??? and directrix y= ??? . So the graph of x2 = 8y is a parabola with focus F(x, y) = and directrix y = -2

Answer 1

You've already mentioned the directrix, so the focus for the parabola
`\(x^2 = 8y\) is \(F(0, 2)\)`.

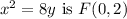Step-by-step explanation:

The equation
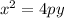`\(x^2 = 4py\)` represents a parabola that opens upward if
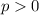`\(p > 0\)` and downward if
`\(p < 0\)`.

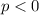For a parabola that opens upward:

1. The focus is at the point
`\(F(0, p)\)`.

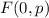2. The directrix is the horizontal line
`\(y = -p\)`.

Given the equation
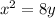`\(x^2 = 8y\)`, we can compare it to the general form
`\(x^2 = 4py\)`:

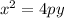From
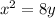`\(x^2 = 8y\)`, we can deduce that
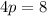`\(4p = 8\)`, which gives
`\(p = 2\)`.

Using the formulas for the focus and directrix:

1. Focus
`\(F(0, p) = F(0, 2)\)`

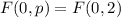
2. Directrix
`\(y = -p = -2\)`

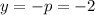
So, for the equation
`\(x^2 = 8y\)`:

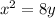- The focus is
`\(F(0, 2)\)`.

- The directrix is
`\(y = -2\)`.

You've already mentioned the directrix, so the focus for the parabola \(x^2 = 8y\) is \(F(0, 2)\).

Answer 2

The focus of the parabola x^2 = 4py is (0, 1/4) and the directrix is y = -1/4.

Step-by-step explanation:

The equation x^2 = 4py represents a parabola. To find the focus and directrix of the parabola, we can compare it to the general equation of a parabola, which is y^2 = 4px. We can see that the coefficients a and b in the general equation are 1 and 4p respectively. By comparing it to x^2 = 4py, we can conclude that p = 1/4. Therefore, the focus of the parabola is (0, 1/4) and the directrix is y = -1/4.