Explanation:
Step 1: Identify the coefficients.
The equation is in the form
 .
.
Here,
 ,
,
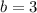 , and
, and
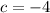 .
.
Step 2: Calculate the discriminant.
The discriminant,
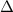 , is given by the formula:
, is given by the formula:
![\[ \Delta = b^2 - 4ac \]](https://img.qammunity.org/2024/formulas/mathematics/college/yt4hy57qyaa50wyopyzfbbj0s52i4qb06m.png)
Plugging in the values we have:
![\[ \Delta = 3^2 - 4(1)(-4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bcprt2k6c64guyiixk0opwwkucrrdjqyro.png)
![\[ \Delta = 9 + 16 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v023abafgrhky5zk19gxicmvqc22yud5vm.png)
![\[ \Delta = 25 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/aa1myeqakb7z8u51g88abqli8terbo2qkm.png)
Step 3: Use the quadratic formula.
The solutions for \(x\) are given by:
![\[ x_1 = (-b + √(\Delta))/(2a) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3wocy9mp4uvh8ym5hiy3d8zkwkdyp17gk3.png)
![\[ x_2 = (-b - √(\Delta))/(2a) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rrnsw4w6o4rf5fedl3gbbtcus42aof5dj3.png)
Using the values for
 ,
,
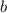 , and
, and
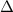 we found:
we found:
![\[ x_1 = (-3 + 5)/(2) = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/oxui7zrt7lqvkyntbw9u4ckmd043xdvmny.png)
![\[ x_2 = (-3 - 5)/(2) = -4 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/et9wqxgr79ec1pg41hpcsfyezlri954v4b.png)
Solution:
The equation
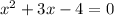 has two solutions:
has two solutions:
![\[ x_1 = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6odh3byac2tnnbs0t0ca695o5mfithimh2.png)
![\[ x_2 = -4 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dn862bc8a291ddko49zw9h0jlbyjm447qt.png)