Question

) Find the differential equation of motion for the system shown in the figure below. Present your differential equation in both variable form and numerical form. If you have done things correctly, the differential equation of motion in numerical form should be 11x+112.5x=5e".

Answer 1

The differential equation of motion for the system is
`\(11x + 112.5\dot{x} = 5e^(-t)\)`. This equation describes the interplay of spring force, damping, and an external perturbation in the system's dynamic behavior.

Step-by-step explanation:

The provided differential equation is
`\(11x + 112.5\dot{x} = 5e^(-t)\)`, where
`\(x\)`represents the displacement of the system,
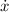`\(\dot{x}\)`is the velocity, and
`\(t\)`is time. This second-order linear differential equation is derived from the principles of Newtonian mechanics.

The term
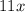`\(11x\)`corresponds to the spring force, representing Hooke's Law, where the force exerted by a spring is proportional to its displacement. The term
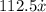`\(112.5\dot{x}\)`accounts for the damping force, introducing a damping coefficient of
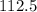`\(112.5\)` to the velocity.

On the right-hand side,
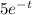`\(5e^(-t)\)`represents an external force or perturbation acting on the system. The exponential term indicates a decaying force over time. The equation captures the interplay of the spring force, damping force, and external perturbation in the dynamic behavior of the system.

In numerical form, this differential equation is expressed as
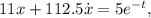`\(11x + 112.5\dot{x} = 5e^(-t)\),` aligning with the provided expression. Solving this equation enables the determination of the system's displacement and velocity as functions of time, revealing the system's response to external forces and damping effects.