Question

Find the domain of the function.
Please put in a step by step answer if you can.

Answer 1

He search
`√(16 - x^2) \geq 0` beacause
`√(x) \geq 0` for all x ∈ R

So we have to solve

`\Leftrightarrow √((x -4)(x+4)) \geq 0`

`\Leftrightarrow x - 4 \geq 0 \ and \ x+4 \leq 0`

`\Leftrightarrow x \geq 4 \ and \ x \leq -4`

So answer D

Answer 2

D. -4 ≤ x ≤ 4

Explanation:

The domain of a function is the set of all real numbers for which the function is defined. In other words, the domain is the set of all inputs that will produce a valid output.

The function
`\sf f(x) =√(16-x^2)` is defined only when the expression under the square root is non-negative.

This means that
`\sf 16 - x^2 \geq 0.`

Solving for x, we get
`\sf x^2 - 16 \leq 0.`

`\sf 16 - x^2 \geq 0`

Add x² to both sides:

`\sf 16 \geq x^2`

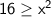
Take the square root of both sides (while considering the positive square root since we're dealing with the domain):

`\sf 4 \geq |x|`

This inequality implies that should be within the range [-4,4} for the function to be defined.

It also can be said as -4 ≤ x ≤ 4

Therefore, the domain of the function
`\sf f(x) =√(16-x^2)` is the interval is :

D. -4 ≤ x ≤ 4