Question

What is the difference between linear and nonlinear

Answer 1

The key difference between linear and nonlinear relationships lies in the patterns they exhibit on a graph. Linear relationships follow a straight line pattern, while nonlinear relationships show more diverse and curved patterns.

Explanation:

In mathematics and science, the terms "linear" and "nonlinear" refer to the behavior or relationship between variables in a given system, equation, or function. Let's delve into each of these concepts:

(1) - Linear:

A linear relationship between variables means that when one variable changes, the other variable changes proportionally, following a straight line pattern on a graph. In other words, if you plot the data points of a linear relationship, they will form a straight line. The general form of a linear equation with two variables (x and y) is represented as:

`\boxed{\left\begin{array}{ccc}\text{\underline{Slope-Intercept Form:}}\\\\ y=mx+b\end{array}\right}`

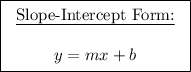
Where:

• "y" is the dependent variable.

• "x" is the independent variable.

• "m" is the slope of the line, representing the rate of change of "y" concerning "x."

• "b" is the y-intercept, indicating the value of "y" when "x" is zero.

For instance, the equation y = 2x + 3 represents a linear relationship with a slope of 2 and a y-intercept of 3.

(2) - Nonlinear:

A nonlinear relationship between variables means that the change in one variable does not follow a straight line pattern concerning the other variable. Instead, it may exhibit various curves, bends, or irregular patterns on a graph. Nonlinear relationships can be more complex and diverse in their behavior.

Examples of nonlinear relationships include quadratic, exponential, logarithmic, and trigonometric functions.

For instance:

• Quadratic:

`y = ax^2 + bx + c`, where "a," "b," and "c" are constants.

• Exponential:

`y=ab^x`, where "a" and "b" are constants and "b" is the base of the exponential function.

• Logarithmic:

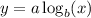`y=a\log_b(x)`, where "a" and "b" are constants and "b" is the base of the logarithm.