Question

Find the supplementary angle in which one angle is 35° more than the other angle.​​

Answer 1

The two angles are 72.5° and 107.5°

Explanation:

Our task is to find the other angle, given that two angles are supplementary. When that's the case, the sum of the angles is 180°.

So, we know that
`\angle1+\angle2=180`.

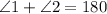We're also given that one angle is 35° more than the other one.

So, we have an equation (where x is the unknown angle)

`x+x+35=180`

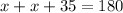
Combine the like terms:

`2x+35=180`

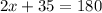
Subtract 35 from both sides:

`2x=145`

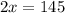
Divide both sides by 2.

`x=72.5`

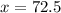
We only have one angle. To find the second one, add 35 to x:

`x+35=72.5+35=107.5^o`

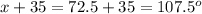
Therefore, the two angles are 72.5° and 107.5°.

Answer 2

72.5° and 107.5°

Explanation:

supplementary angles sum to 180°

let one angle be x then the other angle is x + 35

sum the 2 angles and equate to 180°

x + x + 35 = 180°

2x + 35 = 180° ( subtract 35° from both sides )

2x = 145° ( divide both sides by 2 )

x = 72.5°

and x + 35 = 72.5° + 35° = 107.5°

the supplementary angles are 72.5° and 107.5°