Question

Solve the following differential equation with initial conditions using laplace transforms. sin 4t = ý + 2y Initial conditions : y (0) = 0; y(0) = 3

Answer 1

`y(t) = -(1)/(5)\cos(4t)+(1)/(10)\sin(4t)+(1)/(5)e^(-2t)`

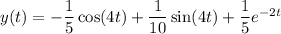
Explanation:

To solve the given differential equation using Laplace transforms, we need to follow these steps:

Step 1: Take the Laplace transform of both sides of the differential equation.

`\boxed{\left\begin{array}{ccc}\text{\underline{Table of basic Laplace Transforms:}}\\1\rightarrow (1)/(s) \\t^n\rightarrow (n!)/(s^(n+1))\\e^(at) \rightarrow(1)/(s-a)\\ \sin(at)\rightarrow(a)/(s^2+a^2)\\\cos(at)\rightarrow(s)/(s^2+a^2)\\e^(at)\sin(bt)\rightarrow(b)/((s-a)^2+b^2)\\e^(at)\cos(bt)\rightarrow(s-a)/((s-a)^2+b^2)\\t^ne^(at)\rightarrow(n!)/((s-a)^(n+1)) \end{array}\right}`

Step 2: Use the properties of Laplace transforms to simplify the equation.

`\boxed{\left\begin{array}{ccc}\text{\underline{Laplace Transforms of DE's:}}\\\\\mathcal{L}\{y''\}=s^2Y(s)-sy(0)-y'(0)\\\\\ \mathcal{L}\{y'\}=sY(s)-y(0) \\\\ \mathcal{L}\{y\}=Y(s)\end{array}\right}`

Step 3: Solve for the Laplace transform of the unknown function y(t).

Step 4: Take the inverse Laplace transform to find the solution y(t).

`\hrulefill`

Given:

`\sin(4t) = y' +2y; \ y(0)=0; \ y'(0)=3`

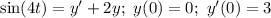
Let's proceed with the solution:

Step 1: Take the Laplace transform of both sides of the differential equation.

`\Longrightarrow \sin(4t) = y' +2y\\\\\\\\\Longrightarrow \mathcal{L}\{\sin(4t)\} = \mathcal{L}\{y' +2y\}\\\\\\\\\Longrightarrow \mathcal{L}\{\sin(4t)\} = \mathcal{L}\{y'\} +\mathcal{L}\{2y\}\\\\\\\\\Longrightarrow \boxed{(4)/(s^2+16) = \mathcal{L}\{y'\} + 2\mathcal{L}\{y\} }`

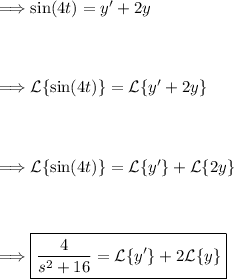
Step 2: Use the properties of Laplace transforms to simplify the equation.

`\Longrightarrow (4)/(s^2+16) = \mathcal{L}\{y'\} + 2\mathcal{L}\{y\}\\\\\\\\\Longrightarrow (4)/(s^2+16) = sY(s) - 0 + 2Y(s)\\\\\\\\\Longrightarrow \boxed{(4)/(s^2+16) = sY(s) + 2Y(s)}`

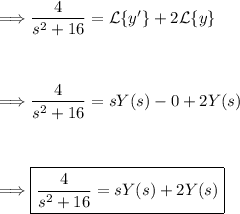
Step 3: Solve for the Laplace transform of the unknown function y(t).

`\Longrightarrow (4)/(s^2+16) = sY(s) + 2Y(s)\\\\\\\\\Longrightarrow (4)/(s^2+16) = Y(s)(s + 2)\\\\\\\\\Longrightarrow Y(s) = (\Big((4)/(s^2+16) \Big))/(s+2) \\\\\\\\\Longrightarrow \boxed{Y(s) = (4)/((s^2+16)(s+2))}`

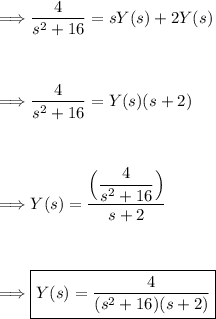
Step 4: Take the inverse Laplace transform to find the solution y(t).

`\Longrightarrow \mathcal{L}\{Y(s)\} = \mathcal{L}\Big\{(4)/((s^2+16)(s+2))\Big\}`

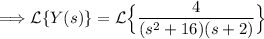
We need to perform partial fraction decomposition on the R.H.S. of the equation in order to take the inverse Laplace transform. So let's walkthrough this:

`\Longrightarrow (4)/((s^2+16)(s+2))=(As+B)/(s^2+16) +(C)/(s+2) \\\\\\\\\Longrightarrow (s^2+16)(s+2)\cdot\Big[(4)/((s^2+16)(s+2))=\frac{As+B} {s^2+16}+(C)/(s+2)\Big]\\\\\\\\\Longrightarrow4=(As+B)(s+2)+C(s^2+16)\\\\\\\\\Longrightarrow4=As^2+2As+Bs+2B+Cs^2+16C\\\\\\\\\Longrightarrow4=(A+C)s^2+(2A+B)s+(2B+16C)`

We get the following system of equations with the unknowns, A, B, and C:

`\Longrightarrow \left\{\begin{array}{ccc}A+C=0\\2A+B=0\\2B+16C=4\end{array}\right`

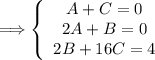
After solving the system, we get:

`A= -(1)/(5), \ B = (2)/(5), \ \& \ C=(1)/(5)`

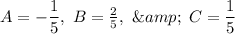
Thus, we have split up the complex fraction. Now we have:

`\Longrightarrow ((-(1)/(5) )s+((2)/(5)))/(s^2+16) +(((1)/(5)))/(s+2) \\\\\\\\\Longrightarrow (2-s)/(5(s^2+16)) +(1)/(5(s+2)) \\\\\\\\\Longrightarrow (-s)/(5(s^2+16))+ (2)/(5(s^2+16)) +(1)/(5(s+2))`

We can now take the inverse Laplace transform of each term separately:

`\Longrightarrow \mathcal{L}^(-1)\{Y(s)\} = \mathcal{L}^(-1)\Big\{(-s)/(5(s^2+16))+ (2)/(5(s^2+16)) +(1)/(5(s+2))\Big\}\\\\\\\\\Longrightarrow y(t) = \mathcal{L}^(-1)\Big\{(-s)/(5(s^2+16))\Big\}+\mathcal{L}^(-1)\Big\{(2)/(5(s^2+16)) \Big\}+\mathcal{L}^(-1)\Big\{(1)/(5(s+2))\Big\}\\\\\\\\\therefore \boxed{\boxed{y(t) = -(1)/(5)\cos(4t)+(1)/(10)\sin(4t)+(1)/(5)e^(-2t)}}`

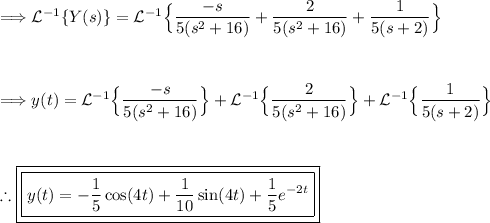
Thus, we have found the particular solution to the given differential equation using Laplace transforms.

`\hrulefill`

Additional Information:

Particular Solution: The particular solution, in the context of Laplace transforms, is the unique solution that satisfies both the given differential equation and the specified initial conditions. The Laplace transform method effectively eliminates the need for arbitrary constants, as it directly leads to the specific solution that meets the initial conditions.