Question

A particle of mass 0. 350 kg is attached to the 100−cm mark of a meterstick of mass 0. 150 kg. The meterstick rotates on the surface of a frictionless, horizontal table with an angular speed of 6. 00rad/s. (a) Calculate the angular momentum of the system when the stick is pivoted about an axis perpendicular to the table through the 50. 0 - cm mark. X kg

2

m

2

/s (b) Calculate the angular momentum of the system when the stick is pivoted about an axis perpendicular to the table through the 0⋅cm mark. X kg+m

2

/s

Answer 1

Assuming that the length of the meter stick is exactly
`1.00\; {\rm m}`.

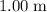(a)
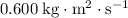`0.600\; {\rm kg\cdot m^(2) \cdot s^(-1)}` when pivoted about the center of the meter stick.

(b)
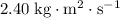`2.40\; {\rm kg\cdot m^(2) \cdot s^(-1)}` when pivoted about the
`100\; {\rm cm}` mark of the meter stick.

Step-by-step explanation:

Angular momentum is the product of moment of inertia and angular velocity. To find the angular momentum of this system under each configuration, start by finding the moment of inertia for the two configurations.

Let
`M = 0.350\; {\rm kg}` denote the mass of the particle, and let
`m = 0.150\; {\rm kg}` denote the mass of the stick.

• For a particle ("satellite") of mass
  `M` moving along a circular path of radius
  `R`, moment of inertia would be
  `M\, R^(2)`.
• For a uniform plank of mass
  `m` length
  `L`, moment of inertia when rotated about the center would be
  `(1/12)\, m\, L^(2)`.
• For the same uniform plank, moment of inertia when rotated about one end of the plank would be
  `(1/3)\, m\, L^(2)`.

In this question, the two objects are fixed together. Since the two objects revolve around the same center, moment of inertia of the combined system is equal to the sum of the moment of inertia of the individual parts.

In configuration (a) where the stick is pivoted at its center:

• At a distance of
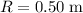  `R = 0.50\; {\rm m}` from the center of rotation, moment of inertia of the particle would be:
  
  `M\, R^(2) = (0.350)\, (0.50)^(2)\; {\rm kg\cdot m^(2)} = 0.0875\; {\rm kg\cdot m^(2)}`.
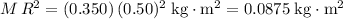• Moment of the inertia of the stick (plank of length
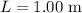  `L = 1.00\; {\rm m}` rotated about the center) would be:
  
  `\displaystyle (1)/(12) m\, L^(2) = (1)/(12)(0.150)\, (1.00)^(2)\; {\rm kg\cdot m^(2)} = 0.0125\; {\rm kg\cdot m^(2)}`.

The total moment of inertia of this combined system would be:

`0.0875\; {\rm kg\cdot m^(2)} + 0.0125\; {\rm kg\cdot m^(2)} = 0.1000\; {\rm kg\cdot m^(2)}`.

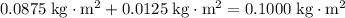The angular momentum of this system under this configuration would be:

`(0.1000\; {\rm kg\cdot m^(2)})\, (6.00\; {\rm s^(-1)}) = 0.600\; {\rm kg\cdot m^(2)\cdot s^(-1)}`.

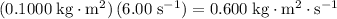Similarly, in configuration (b) where the stick is pivoted at its center:

• At a distance of
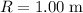  `R = 1.00\; {\rm m}` from the center of rotation, moment of inertia of the particle would be:
  
  `M\, R^(2) = (0.350)\, (1.00)^(2)\; {\rm kg\cdot m^(2)} = 0.350\; {\rm kg\cdot m^(2)}`.
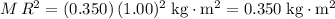• Moment of the inertia of the stick (plank of length
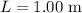  `L = 1.00\; {\rm m}` rotated about one of the two ends) would be:
  
  `\displaystyle (1)/(3) m\, L^(2) = (1)/(3)(0.150)\, (1.00)^(2)\; {\rm kg\cdot m^(2)} =0.050\; {\rm kg\cdot m^(2)}`.

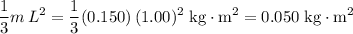The total moment of inertia of this combined system would be:

`0.350\; {\rm kg\cdot m^(2)} + 0.050\; {\rm kg\cdot m^(2)} = 0.400\; {\rm kg\cdot m^(2)}`.

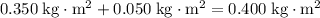The angular momentum of this system under this configuration would be:

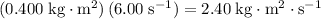`(0.400\; {\rm kg\cdot m^(2)})\, (6.00\; {\rm s^(-1)}) =2.40\; {\rm kg\cdot m^(2)\cdot s^(-1)}`.