Question

Show that the three points P(2, 4), Q(4, 6) and R(6, 8) are collinear.​

Answer 1

see explanation

Explanation:

if 3 or more points are collinear , then they lie on the same line

if the 3 points are collinear then the slope m between consecutive points should be equal.

calculate the slope m using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

with (x₁, y₁ ) = P (2, 4 ) and (x₂, y₂ ) = Q (4, 6 )

`m_(PQ)` =
`(6-4)/(4-2)` =
`(2)/(2)` = 1

repeat with

(x₁, y₁ ) = Q (4, 6 ) and (x₂, y₂ ) = R (6, 8 )

`m_(QR)` =
`(8-6)/(4-2)` =
`(2)/(2)` = 1

since
`m_(PQ)` =
`m_(QR)` = 1

then the 3 points are collinear

Answer 2

The points are collinear because the slopes of all three-line segments connecting them are equal.

Explanation:

Definition of collinear points

Three or more points are said to be collinear if they lie on the same line.

One way is to show that the slopes of the line segments connecting any two of the points are equal.

For The Question:

Showing that P(2, 4), Q(4, 6), and R(6, 8) are collinear.

Let's start by finding the slopes of the line segments connecting P(2, 4), Q(4, 6), and R(6, 8).

We can use this formula:

`\sf m =( (y_2 - y_1) )/( (x_2 - x_1))`

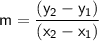
where:

• m is the slope of the line
• y2 and y1 are the y-coordinates of the two points
• x2 and x1 are the x-coordinates of the two points

The slope of the line segment connecting P and Q is:

`\sf slope = ((6 - 4))/((4 - 2)) =1`

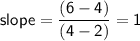
The slope of the line segment connecting Q and R is:

`\sf slope = ((8 - 6))/((6 - 4) ) = 1`

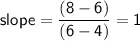
Since the slopes of the two-line segments are equal, we know that the three points P, Q, and R lie on the same line.

Therefore, the three points are collinear.