Question

Prove:


`1+cot^2x=csc^2x`

Answer 1

To answer this question you need to know a couple important Trigonometric Identities.

1
`sin^2x+cos^2x = 1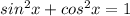` --- Pythagorean(most important)

2.
`1+cot^2x = csc^2x`

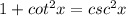
3.
`1+tan^2x = sec^2x`

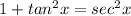
The first step is realising that
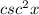`csc^2x` is the same as
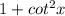`1+cot^2x`. And you also have to realize that
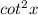`cot^2x` is the same as
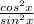`(cos^2x)/(sin^2x)`. So, we can deduce that:

`csc^2x = 1+(cos^2x)/(sin^2x)`

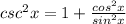
The second step is eliminating the 1, and the rest is common sense, we get a common denominator, use our pythagorean theorem of Trigonometry, and flip the fraction to get:

`csc^2x`

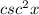
I am sorry for using x and "∅" interchangably.

The full steps are in the attachment.