Answer: The function has two roots in common.
Explanation:
To determine how many roots the function
 has, we can find its discriminant. The discriminant will tell us the nature of the roots:
has, we can find its discriminant. The discriminant will tell us the nature of the roots:
1. If
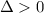 , the quadratic has two distinct real roots.
, the quadratic has two distinct real roots.
2. If
 , the quadratic has one real root (a repeated root).
, the quadratic has one real root (a repeated root).
3. If
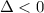 , the quadratic has no real roots (two complex conjugate roots).
, the quadratic has no real roots (two complex conjugate roots).
The discriminant
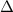 for a quadratic equation of the form
for a quadratic equation of the form
 is given by:
is given by:
![\[ \Delta = b^2 - 4ac \]](https://img.qammunity.org/2024/formulas/mathematics/college/yt4hy57qyaa50wyopyzfbbj0s52i4qb06m.png)
For the function
 :
:
a = 1
b = -4
c = -5
Plugging in these values:
![\[ \Delta = (-4)^2 - 4(1)(-5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pg5f0mep6ooj80rr7x2vxz4fqro98c6ojr.png)
Let's calculate the value of
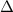 to determine the number of roots.
to determine the number of roots.
The discriminant
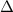 for the function
for the function
 is:
is:
![\[ \Delta = 36 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b6sxs2dq243gd5vld7k5crfdid6cayxte7.png)
Since
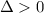 , the quadratic function
, the quadratic function
 has two distinct real roots.
has two distinct real roots.
Thus, the function has two roots in common.