Question

Can anybody help me solve this problem step by step​

Answer 1

Answer: The limit of
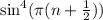`\( \sin^4(\pi (n + (1)/(2))) \)` as
`\( n \)` approaches infinity is indeterminate. This means that the function does not approach a specific value as
`\( n \)` goes to infinity.

Explanation:

Given the function:

`\[ f(n) = \sin^4(\pi (n + (1)/(2))) \]`

We want to find:

`\[ \lim_{{n \to \infty}} f(n) \]`

Step 1: Understand the inner function

The inner function is
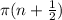`\( \pi (n + (1)/(2)) \)`. As
`\( n \)` approaches infinity, this term will also approach infinity. This means the argument of the sine function will take on increasingly larger values.

Step 2: Behavior of the sine function

The sine function oscillates between -1 and 1 for all real numbers. Specifically,
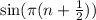`\( \sin(\pi (n + (1)/(2))) \)` will always be -1 or 1 because:

`\[ \sin(\pi/2) = 1 \]`

\[ \sin(3\pi/2) = -1 \]

... and so on for every integer value of
`\( n \)`.

Step 3: Raising to the fourth power

Regardless of whether
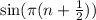`\( \sin(\pi (n + (1)/(2))) \)` is 1 or -1, when you raise it to the fourth power, the result will always be 1. This is because:

`\[ 1^4 = 1 \]`

`\[ (-1)^4 = 1 \]`

Step 4: Conclusion

Given that for all integer values of
`\( n \)`,
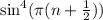`\( \sin^4(\pi (n + (1)/(2))) \)` will always be 1, the limit as
`\( n \)` approaches infinity is also 1.

`\[ \lim_{{n \to \infty}} \sin^4(\pi (n + (1)/(2))) = 1 \]`