Question

Help What is the discriminant of 3x2 - 10x = -2?

Answer 1

Answer: The discriminant is 76.

Explanation:

To find the discriminant of a quadratic equation, we first need to express the equation in the standard form:

`\[ ax^2 + bx + c = 0 \]`

Given the equation:

`\[ 3x^2 - 10x = -2 \]`

Rearrange it to get:

`\[ 3x^2 - 10x + 2 = 0 \]`

From the equation, we can identify:

a = 3

b = -10

c = 2

The discriminant,
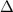`\( \Delta \)`, of a quadratic equation
`\( ax^2 + bx + c = 0 \)`is given by:

`\[ \Delta = b^2 - 4ac \]`

Plugging in the values we have:

`\[ \Delta = (-10)^2 - 4(3)(2) \]`

The discriminant
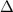`\( \Delta \)` of the equation
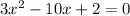`\( 3x^2 - 10x + 2 = 0 \)` is:

`\[ \Delta = 76 \]`

So, the discriminant is 76.