Question

Please help and explain how you worked it out. i am lost!

thankyou so much

Answer 1

Explanation:

When x = 1 y = 0

the only equation that satisfies this is top right y= x^2 +2x -3

When x =1 y = 0 as the graph shows

Answer 2

Answer:
`y=x^(2)+2x-3`

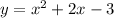
Explanation:

To solve this we need to take a look at the graph. We can see the graph has it's vertex point at (-1,-4). That means the transformations would have been left 1 and down 4.

The standard vertex form is
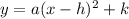`y=a(x-h)^(2)+k` where a controls stretch or compression, k controls up or down, and h controls left or right. In vertex from that would be
`y=1(x+1)^(2)-4`.

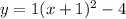From there, we can transform this into quadratic standard form. This is
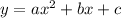`y=ax^(2)+bx+c`. The first step would be to turn (x+1)² into a trinomial. To do that multiply (x+1) with (x+1) since (x+1) is squared.

(x+1)(x+1):

x·x=x²

x·1=x

1·x=x

1·1=1

Now the equation is
`y=x^(2)+x+x+1-4`.

Now, just combine like terms. x+x=2x and 1-4=-3. The final equation will be

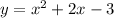`y=x^(2)+2x-3` that way.

Hope that helped very much.

:)