Answer:
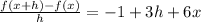 where
where
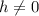
Explanation:
To find the difference quotient for the function
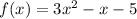 , we'll use the formula:
, we'll use the formula:
![\[ (f(x+h) - f(x))/(h) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/es2ljrypn83qub85re3u2dhz78pc682jbc.png)
Step 1: Find
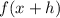
![\[ f(x+h) = 3(x+h)^2 - (x+h) - 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jhjbt353eehued3ouwoy7fj8u4tikd1s0c.png)
Step 2: Subtract
 from
from
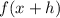
![\[ f(x+h) - f(x) = 3(x+h)^2 - (x+h) - 5 - (3x^2 - x - 5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8x3mti564s4ke7846vk606c27fdd3t72u2.png)
Step 3: Divide the result from Step 2 by

![\[ (f(x+h) - f(x))/(h) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/es2ljrypn83qub85re3u2dhz78pc682jbc.png)
Let's plug in the values and simplify.
The simplified difference quotient for the function
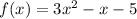 is:
is:
![\[ (f(x+h) - f(x))/(h) = -1 + 3h + 6x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wktqrq22zqqjr43mjdbfj82umyqlu7u63e.png)
So,
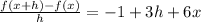 where
where
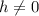 .
.