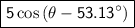Question

Can someone provide how to do this any help will be appreciated :]

Answer 1

`5 \cos(\theta - 53.1^(\circ))`

Explanation:

To express a cos θ + b sin θ in the form R cos(θ - α), use the cosine R formula:

`\boxed{a \cos \theta \pm b \sin \theta \equiv R \cos (\theta \mp \alpha)}`

where a, b and R are positive, and α is acute.

`\hrulefill`

Given:

`3 \cos \theta + 4 \sin \theta =R \cos(\theta - \alpha)`

Expand the right side using the addition formula:

`\boxed{\cos(A-B)\equiv \cos A \cos B+\sin A \sin B}`

Therefore:

`3 \cos \theta + 4 \sin \theta =R \cos \theta \cos\alpha + R \sin\theta \sin\alpha`

Equate the coefficients of cos θ and sin θ:

`\begin{aligned}\textcircled{1}\quad 3 \cos \theta &=R \cos \theta \cos\alpha\\3&=R\cos\alpha\end{aligned}`

`\begin{aligned}\textcircled{2}\quad 4 \sin\theta &=R \sin\theta \sin\alpha\\4&=R\sin\alpha\end{aligned}`

To find α, divide equation 2 by equation 1:

`(R \sin \alpha)/(R \cos \alpha)=(4)/(3)`

`\tan \alpha=(4)/(3)`

`\alpha=\tan^(-1)\left((4)/(3)\right)`

`\alpha=53.130102354...^(\circ)`

`\alpha=53.1^(\circ)\; \sf (3\;s.f.)`

To find R, square equations 1 and 2 and add them together, then solve for R:

`\begin{aligned}(R\cos\alpha)^2 +(R\sin\alpha)^2 &= 3^2+4^2\\R^2\cos^2\alpha+R^2\sin^2\alpha&=9+16\\R^2(cos^2\alpha+\sin^2\alpha)&=25\\R^2(1)&=25\\R^2&=25\\√(R^2)&=\srt{25}\\R&=5\end{aligned}`

Finally, substitute the values of α and R into the identity to give:

`\large\boxed{3 \cos \theta + 4 \sin \theta =5 \cos(\theta - 53.1^(\circ))}`

Answer 2

`\boxed{\sf 5 \cos \left( \theta - 53.13^\circ \right)}`

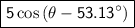
Explanation:

Defination used here:

• Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
• Arctangent function: The arctangent function is the inverse of the tangent function. It takes an angle as input and returns the corresponding tangent value.
• Magnitude: The magnitude of a vector is its length. In the case of the expression 3 cos θ + 4 sinθ, the magnitude is the length of the hypotenuse of the right triangle

`\hrulefill`

For The Question:

In order to express
`\sf 3 \cos \theta + 4 \sin \theta` in the desired form
`\sf R \cos (\theta - a),` where R > 0 and
`\sf 0 < a < 90^\circ` , we can follow these steps:

Let's calculate the magnitude R first.

The magnitude R is the length of the hypotenuse of a right triangle with legs of length 3 and 4.

We can calculate it using the Pythagorean theorem:

`\sf R^2 = 4^2 + 3^2`

`\sf R^2= 16+9`

`\sf R^2 = 25`

`\sf R=√(25)`

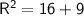
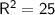
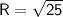
Therefore, R= 5.

Now,

Calculate the angle a.

The angle a is the angle between the hypotenuse and the side of length 5.

We can calculate it using the arctangent function:

`\sf a =\tan^(-1) \left( (4)/(3) \right)`

`\sf a \approx 53.13`

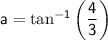
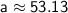
The arctangent function takes the ratio of the opposite side to the adjacent side of a right triangle and returns the angle that corresponds to that ratio.

In this case, the opposite side is 4 and the adjacent side is 3, so the angle is approximately 53.13°.

Now,

Expressing the expression in the desired form.

Now that we know

R = 5 and a =53.13°

we can express the expression as follows:

`\sf 3 \cos \theta + 4 \sin \theta = 5 \cos \left( \theta - 53.13^\circ \right)`

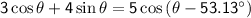
Therefore, the expression
`\sf 3 \cos \theta + 4 \sin \theta` can be written in the form:

`\boxed{\sf 5 \cos \left( \theta - 53.13^\circ \right)}`

`\underline{\red{\textsf{Happy To Help }}}`