Question

A trucker drove 175 miles to make a delivery and returned home on the same route. because of foggy conditions, his average speed on the return trip was 10 mph less than his average speed going. If the return trip took 2 hours longer, how fast did he drive in each direction?

Answer 1

Answer: The trucker drove at an average speed of 35 mph to the delivery and 25 mph on the return trip.

Explanation:

Let's call the trucker's average speed on the way to the delivery
`\( x \)`mph. So, on the return trip, his average speed would be
`\( x - 10 \)` mph due to the foggy conditions.

1. Time taken to drive to the delivery
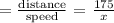`= \( \frac{\text{distance}}{\text{speed}} \) = \( (175)/(x) \)` hours.

2. Time taken to return home
`= \( (175)/(x - 10) \)` hours.

Given that the return trip took 2 hours longer than the trip to the delivery, we can set up the following equation:

`\[ (175)/(x - 10) = (175)/(x) + 2 \]`

Now, let's solve for \( x \) to find the average speed on the way to the delivery.

From the solution, we have two potential values for
`\( x \)`: -25 and 35. However, a negative speed doesn't make sense in this context, so we'll discard the -25 value.

Thus, the trucker's average speed on the way to the delivery was
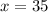`\( x = 35 \)` mph. On the return trip, due to the foggy conditions, his average speed was
`\( x - 10 = 25 \)` mph.

So, the trucker drove at an average speed of 35 mph to the delivery and 25 mph on the return trip.