Question

The first term in an arithmetic series is 2, while the sum of the first 8 terms of the series is 1472. What is the 8th term in the series?​

Answer 1

8th term in the arithmetic series is 366.

Explanation:

In order to find the 8th term in the arithmetic series, we can use the formula for the sum of the first n terms of an arithmetic series and then use that information to find the 8th term.

The formula for the sum of the first n terms of an arithmetic series is given by:

`\boxed{\sf Sum = (n)/(2)* (first \:term + last\: term)}`

Let's denote the first term of the series as 'a'

The common difference between consecutive terms as 'd'.

The first term 'a' is given as 2.

So, the sum of the first 8 terms (n = 8) is 1472:

Substituting value

`\sf 1472 = (8)/(2)* (2 + last \:term)`

`\sf 1472 = 4 * (2 + last\: term)`

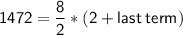
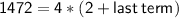
Divide both sides by 4:

`\sf (1472)/(4) = 2 + last term`

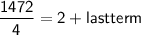
368 = 2 + last term

Subtract 2 from both sides:

last term = 368 - 2

last term = 366

Therefore, the 8th term in the arithmetic series is 366.