Question

Hi i need help with further trig. im not sure how to start off with part (a)

Answer 1

a = 24

d(t) = 25 cos (3πt-0.28)

t = 0.15, 0.57, 0.82

X max = 65 mm

X min = 15 mm

Step-by-step explanation:

d(t) = a cos 3πt + 7 sin 3πt

= R cos (3πt-φ)

where
`R=√(a^2+7^2)` &
`tan\ \phi=(7)/(a)`

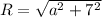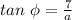
(a)

d(t) max → [R cos (3πt-φ)] max → cos (3πt-φ) = 1

d(t) max = R × 1

25 = R

25 =
`√(a^2+7^2)`

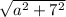
625 = a² + 49

a = √576

= 24

(b)

`R=√(a^2+7^2)`

`=√(24^2+7^2)`

`=25`

`tan\ \phi=(7)/(a)`

`=(7)/(24)`

`\phi=tan^(-1)((7)/(24))`

`= 0.28\ rad`

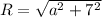
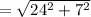
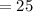
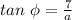
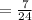
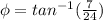
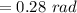
d(t) = 25 cos (3πt-0.28)

(c)

d(t) = 25 cos (3πt-0.28)

10 = 25 cos (3πt-0.28)

cos (3πt-0.28) = 0.4

3πt - 0.28 = ±1.16 + 2πk

(i) 3πt = 1.44 + 2πk

`t=(1.44+2\pi k)/(3\pi)`

= 0.15 +
`(2)/(3) k`

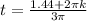
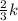
= 0.15, 0.82

(ii) 3πt = -0.88 + 2πk

`t=(-0.88+2\pi k)/(3\pi)`

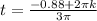
= -0.09 +
`(2)/(3) k`

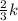
= 0.57

∴ t = 0.15, 0.57, 0.82

(d)

X max → R = 25

X max = FO + 25

= 40 + 25

= 65 mm

X min → R = -25

X min = FO - 25

= 40 - 25

= 15 mm