Question

The height of a ball t seconds after it is thrown is modeled by the function h(t)=15t-4.9t^2 +3, where h is the height of the ball in meters. For what length of time will the ball be higher than 12 meters?

Answer 1

The ball will be higher than 12 meters for t values greater than 3 seconds.

Explanation:

We have the function: h(t) = 15t - 4.9t^2 + 3

We want to find when the height is greater than 12 meters, so we set up the inequality:

15t - 4.9t^2 + 3 > 12

Now, let's solve this inequality:

15t - 4.9t^2 + 3 - 12 > 0

-4.9t^2 + 15t - 9 > 0

To solve this quadratic inequality, we can use factoring, the quadratic formula, or graphing. In this case, let's use factoring:

-4.9t^2 + 15t - 9 = 0

Now, we need to find the roots of this equation:

(-4.9t + 3)(t - 3) > 0

To determine when the inequality is true, we need to consider the sign of each factor:

-4.9t + 3 > 0 and t - 3 > 0

Solving each inequality separately:

-4.9t + 3 > 0

t < 3/4.9

t < 0.6122...

t - 3 > 0

t > 3

So, the ball will be higher than 12 meters for t values greater than 3 seconds.

Answer 2

1.42 s

Explanation:

Given function:

`\large\boxed{h(t)=15t-4.9t^2 +3}`

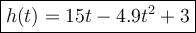
where:

• h is the height of the ball (in meters).
• t is the time after the ball is thrown (in seconds.

To find the length of time that the ball will be higher than 12 meters, we need to find the times when the ball will be 12 meters, then calculate the difference.

To find the time (t) when the ball will be 12 meters, substitute h(t) = 12 into the function:

`15t-4.9t^2 +3=12`

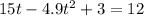
Rearrange to form a quadratic function in the form ax² + bx + c = 0:

`\begin{aligned}15t-4.9t^2 +3&=12\\15t-4.9t^2-9&=0\\4.9t^2-15t+9&=0\end{aligned}`

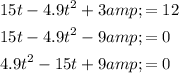
To solve for t, use the quadratic formula.

`\boxed{\begin{array}{l}\underline{\text{Quadratic \;Formula}}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\text{when} \;ax^2+bx+c=0\\\\\end{array}}`

In this case, the values of a, b and c are:

• a = 4.9
• b = -15
• c = 9

Substitute the values of a, b and c into the quadratic formula, and solve for t:

`t=(-(-15)\pm √((-15)^2-4(4.9)(9)))/(2(4.9))`

`t=(15\pm √(225-176.4))/(9.8)`

`t=(15\pm √(48.6))/(9.8)`

`t=(75\pm 9√(15))/(49)`

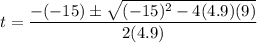
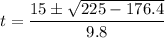
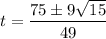
Therefore, the two values of t are:

`t=2.24197653...`

`t=0.819247956...`

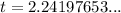
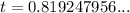
So the ball is at 12 meters at 0.82 seconds and 2.24 seconds.

To find the length of time the ball will be higher than 12 meters, calculate the positive difference between the two times.

`t=2.24197653...-0.819247956...`

`t=1.42272857...`

`t=1.42\; \sf s\;(3\;s.f.)`

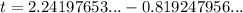
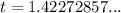
Therefore, the ball will be higher than 12 meters for 1.42 s.