Answer:
Radius = 12 cm
Explanation:
Note:
In geometry, a tangent is a line that touches a circle at exactly one point. The point of contact is called the point of tangency. The tangent line is perpendicular to the radius drawn to the point of tangency.
For the Question:
In the given figure, CP is the radius of the circle.
Given:
To find:
Solution:
Since PT is a tangent to the circle, CP is perpendicular to PT.
Therefore, in triangle PCT is right angled triangle.
In right angled triangle PCT
- Hypotenuse = PC = 20 cm
- Base = PT = 16 cm
- Perpendicular = TC = radius = ?
Now,
We can use Pythagoras theorem,
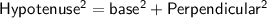
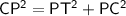
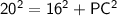
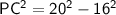
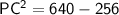
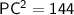
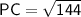
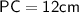
Therefore, the radius of the circle is 12 cm.