Answer: The slope is 3/4
Explanation:
Our task is to find the slope of the line that is perpendicular to the one whose equation is
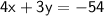 .
.
First, let's rewrite this equation in slope-intercept form:
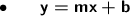
Subtract
 from both sides.
from both sides.
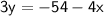
Divide both sides by 3.
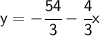
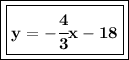
Here's the line's equation. Now, what is the slope of the line that's perpendicular to the one whose equation we just found?
You may recall that perpendicular lines have slopes that are negative inverses of one another. The opposite inverse of -4/3 is 3/4.