Question

Solve. (6√6)^(−x+3) =1/6⋅216^(2x−3) Enter your answer in the box. Enter any fraction as a simplified fraction. x= ________

Answer 1

The equation
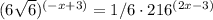`(6√(6))^((-x+3)) = 1/6\cdot216^((2x-3))` can be simplified by expressing both sides with the same base of 6. Upon combining the exponents, we equate them since the bases are the same, leading to the solution x = 1.

Step-by-step explanation:

We have the equation
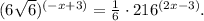`(6√(6))^((-x+3)) = (1)/(6)\cdot216^((2x-3)).` First, let's simplify the right side of the equation by recognizing that 216 is a power of 6, specifically
`6^3`. This will help us to base both sides of the equation with the same base for easier comparison of the exponents.

Now the equation looks like this:
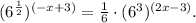`(6^{(1)/(2)})^((-x+3)) = (1)/(6)\cdot(6^3)^((2x-3)).`Simplifying the powers of 6 gives us:
`6^{(-(1)/(2)x + (3)/(2))} = 6^(-1)\cdot6^((6x-9)).`

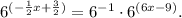
Combine the exponents on the right:
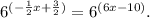`6^{(-(1)/(2)x + (3)/(2))} = 6^((6x-10)).` Since the bases are the same, the exponents must be equal: -
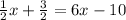`(1)/(2)x + (3)/(2) = 6x - 10`. Solving for x gives us
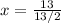`x = (13)/(13/2)`, which simplifies to x = 1. Therefore, the solution is x = 1.