Question

Which graph shows the solution to the system of linear equations? y equals one third times x x + 3y = −6 coordinate plane with one line that passes through the points 0 comma negative 4 and 2 comma negative 5 and another line that passes through the points 0 comma 0 and 2 comma 1 coordinate plane with one line that passes through the points 0 comma 2 and negative 3 comma 3 and another line that passes through the points 0 comma 0 and negative 3 comma negative 1 coordinate plane with one line that passes through the points 3 comma negative 3 and 0 comma negative 2 and another line that passes through the points 0 comma 0 and 3 comma 1 coordinate plane with one line that passes through the points 0 comma 4 and negative 1 comma 1 and another line that passes through the points 0 comma 0 and 1 comma 3

Answer 1

C) Coordinate plane with one line that passes through the points (3, -3) and (0, -2) and another line that passes through the points (0, 0) and (3, 1).

Explanation:

The given system of linear equations is:

`\begin{cases}y=(1)/(3)x\\\\x+3y=-6\end{cases}`

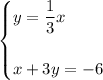
The solution to a system of linear equations is the point where the graphs intersect.

To find the solution to the given system of linear equations algebraically, substitute the first equation into the second equation and solve for x:

`\begin{aligned}x+3\left((1)/(3)x\right)&=-6\\\\x+x&=-6\\\\2x&=-6\\\\(2x)/(2)&=(-6)/(2)\\\\x&=-3\end{aligned}`

Substitute the found value of x into the first equation and solve for y:

`\begin{aligned}y&=(1)/(3)(-3)\\\\y&=-1\end{aligned}`

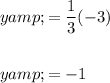
Therefore, the solution to the given system of equations is (-3, -1).

The first equation represents a direct variation, and therefore passes through the origin (0, 0). The slope of this line is positive, and as x increases by 3 units, y increases by 1 unit. Therefore, this line passes through point (3, 1).

Rearrange the second equation so that it is in slope-intercept form:

`\begin{aligned}x+3y&=-6\\3y&=-x-6\\y&=-(1)/(3)x-2\end{aligned}`

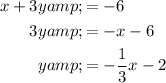
We can see that the second equation has a negative slope of -1/3, which means that as x increases by 3 units, y decreases by 1 unit. The y-intercept is y = -2, which means the line passes through point (0, -2). When x = 3, y = -3, so the line passes through point (3, -3).

Therefore, the graph that shows the solution to the given system of linear equations is:

• C) Coordinate plane with one line that passes through the points (3, -3) and (0, -2) and another line that passes through the points (0, 0) and (3, 1).