Question

Imagine you put $1,000 on furniture for your new apartment. The furniture store advertises 10% APR and no payments for one year , but you forgot to check how often it's compounded .

Answer 1

The interest on the $1,000 furniture purchase with a 10% APR compounded annually for one year is $100.

Step-by-step explanation:

Compounding interest is crucial in determining the total amount paid on a loan or purchase. In this case, the Annual Percentage Rate (APR) is 10%, meaning that interest is calculated on the initial principal of $1,000. Since the compounding frequency is not specified, we assume it's compounded annually. The formula for compound interest is given by:

`\[ A = P * (1 + (r)/(n))^(n * t) \]`

Where:

-
`\( A \)` is the final amount,

-
`\( P \)` is the principal (initial amount),

-
`\( r \)` is the annual interest rate (as a decimal),

-
`\( n \)` is the number of times interest is compounded per year, and

-
`\( t \)` is the time the money is invested or borrowed in years.

In our case,
`\( P = $1,000 \), \( r = 0.10 \)` (10% as a decimal),
`\( n = 1 \)` (compounded annually), and
`\( t = 1 \)`year. Plugging these values into the formula:

`\[ A = $1,000 * (1 + (0.10)/(1))^(1 * 1) \]`

Simplifying this expression gives us
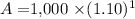`\( A = $1,000 * (1.10)^1 \)`, which results in
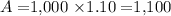`\( A = $1,000 * 1.10 = $1,100 \)`. The interest earned is the difference between the final amount and the initial principal:
`\( $1,100 - $1,000 = $100 \)`.

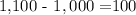Therefore, the interest accrued on the $1,000 furniture purchase with a 10% APR compounded annually for one year is $100.