Final Answer:
The height of the hill is approximately
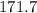 feet.
feet.
Step-by-step explanation:
Let's denote the height of the hill as
 and the distance from the person to the bottom of the antenna as
and the distance from the person to the bottom of the antenna as
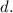
Using trigonometry, we can set up two equations based on the given information:
1. The tangent of the angle of elevation
 to the bottom of the antenna is given by:
to the bottom of the antenna is given by:
![\[ \tan(\theta) = (h)/(d) \]](https://img.qammunity.org/2024/formulas/physics/high-school/a9ngmva0ayqril6lpl124dfm4ktc7b6hc5.png)
In this case,
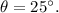
2. The tangent of the angle subtended by the antenna
 is given by:
is given by:
![\[ \tan(\alpha) = \frac{\text{height of antenna}}{\text{distance to antenna}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/j4kpw00mxc6q8u750ghwq632xl8qebw1o7.png)
In this case,
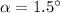 and the height of the antenna is
and the height of the antenna is
 feet.
feet.
Now, solve these equations simultaneously to find

![\[ \tan(25^\circ) = (h)/(d) \]](https://img.qammunity.org/2024/formulas/physics/high-school/1y205m5f7ieziqx0r0hzxiqt97orjz3uh1.png)
![\[ \tan(1.5^\circ) = (121)/(d) \]](https://img.qammunity.org/2024/formulas/physics/high-school/1a181ds24sxh3udno4wqcyens25hsepmmd.png)
Solving the first equation for
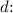
![\[ d = (h)/(\tan(25^\circ)) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ak3shvib4oq2bcmwnbfk58z3gigoqudgcv.png)
Substitute this expression for
 into the second equation:
into the second equation:
![\[ \tan(1.5^\circ) = (121)/((h)/(\tan(25^\circ))) \]](https://img.qammunity.org/2024/formulas/physics/high-school/pbg7b2gj9z56wtjvswsfxtmsqhxoviw4j4.png)
Now, solve for

![\[ h = (121 \cdot \tan(25^\circ))/(\tan(1.5^\circ)) \]](https://img.qammunity.org/2024/formulas/physics/high-school/mhl9zshn20invjv667uw9fsdy4sofl654m.png)
Calculating this expression gives
 feet.
feet.
Therefore, the height of the hill is approximately
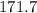 feet.
feet.