Question

FInd the exact value of COT(thata) for and handle that with SIN (that) =-1/6 and with its terminal side in quadrent lll.

Answer 1

`-√(35)`

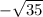
Explanation:

To find the exact value of cotangent (cot) theta when sine (sin) theta is equal to -1/6 and the terminal side of the angle is in quadrant III, we can use the relationship between cotangent and sine functions.

We know that cot(theta) is the reciprocal of tan(theta), and tan(theta) is defined as the ratio of sine(theta) to cosine(theta). Using this information, we can follow these steps to find the value of cot(theta):

Step 1: Determine the cosine (cos) value of theta.

Since sine(theta) is given as -1/6 and the terminal side of the angle is in quadrant III, we know that the sine function is negative in this quadrant. By using the Pythagorean identity sin^2(theta) + cos^2(theta) = 1, we can solve for cos(theta).

sin^2(theta) = (-1/6)^2 = 1/36

cos^2(theta) = 1 - sin^2(theta) = 1 - 1/36 = 35/36

cos(theta) = sqrt(35/36)

Step 2: Calculate the cotangent (cot) value of theta.

cot(theta) = 1 / tan(theta)

tan(theta) = sin(theta) / cos(theta) = (-1/6) / (sqrt(35/36)) = -sqrt(36/35) / 6 = -sqrt(36) / (6 * sqrt(35)) = -6 / (6 * sqrt(35)) = -1 / sqrt(35)

cot(theta) = 1 / (-1 / sqrt(35)) = -sqrt(35)

Therefore, the exact value of cot(theta) for sin(theta) = -1/6, with the terminal side of the angle in quadrant III, is -sqrt(35).

Answer 2

-sqrt(35)/6 or -0.986

Explanation:

sin(Θ) = -1/6

We can use the trig identity that sin^2(Θ)+cos^2(Θ) = 1

Plugging in the value of sinΘ, we find that 1/36+cos^2(Θ) = 1, so cos^2(Θ) = 1-1/36 = 35/36.

Absolute Value of Cos(Θ) = sqrt(35/36) = sqrt(35)/6 ≈ 0.986.

However, since we know that cosine theta is in the 3rd quadrant, we know that it must be the negative square root.

So the answer of cos(Θ) = -0.986 = -sqrt(35)/6