Question

50P HELP PLEASE >>> What are the domain and range of the function:

f(x) = x^4 - 2x^2 - 4?

A.domain: all real numbers range: all real numbers greater than or equal to –5
B.domain: all real numbers range: all real numbers greater than or equal to –4
C.domain: all real numbers between –2.5 and 2.5 range: all real numbers
D.domain: all real numbers between –2.5 and 2.5 range: all real numbers greater than or equal to –5

Answer 1

Explanation:

let f(x)=y

`y=x^4-2x^2-4=x^4-2x^2+1-1-4=(x^2-1)^2-5\\Range:all~real~numbers~\geq -5\\domain :all~real~numbers`

Answer 2

A. domain: all real numbers

range: all real numbers greater than or equal to –5

Explanation:

Given function:

`\sf f(x) = x^4 - 2x^2 - 4`

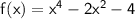
To find domain.

We know that the domain of a function is the set of input values for f, in which the function is real and defined.

The given function has no undefined values of x.

Thus, for the given function, the domain is the set of all real numbers.

Domain = [-∞, ∞]

`\hrulefill`

To find the range,

let
`\sf y = x^4 - 2x^2 - 4` and solve for x:

`\sf y + 4 = x^4 - 2x^2`

`\sf x^4 - 2x^2 - (y + 4) = 0`

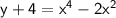
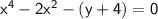
This is a quadratic equation in terms of
`\sf x^2.`

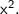
The solutions for
`\sf x^2` will be real when the discriminant is non-negative:

`\sf Discriminant = b^2 - 4ac`

`\sf Discriminant = (-2)^2 - 4(1)(-(y + 4)) = 4 + 4(y + 4) = 4(1 +y + 4)=4(y+5)`

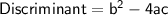
For real solutions, the discriminant must be greater than or equal to zero:

4(y + 5) ≥ 0

y + 5 ≥ 0

y ≥ -5

So, the range of the function f(x) = x^4 - 2x^2 - 4 is all real numbers greater than or equal to -5.

Range: [-5, ∞)

Therefore, the correct answer is:

A. domain: all real numbers

range: all real numbers greater than or equal to –5

Mathematically

Domain: (-∞, ∞)

Range: [-5, ∞)