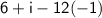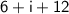2 Answers

Mads · Answer 1 · 2024-01-07T15:18:59+0000

Answer: 18 + i

Explanation:

Hello :) Our task is to simplify the following complex expression:

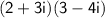$\sf{(2+3i)(3-4i)}$ .

We multiply two complex numbers just like we multiply any two binomials. We use the same method called FOIL.

FOIL

First terms:
$\sf{2*3=6}$

Outer terms:
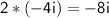
$\sf{2*(-4i)=-8i}$

Inner terms:
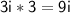
$\sf{3i*3=9i}$

Last terms:
$\sf{3i*(-4i)=-12i^2}$

We have:

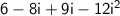
$\sf{6-8i+9i-12i^2}$

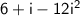
$\sf{6+i-12i^2}$

Recall that i^2 = -1:

$\sf{6+i-12(-1)}$

$\sf{6+i+12}$

$\sf{18+i}$

Please log in or register to add a comment.