Question

A scientist has two solutions, which she has labeled solution A and solution B. Each contains salt. She knows that solution A is 30% salt and solution B is 75% salt. She wants to obtain 180 ounces of a mixture that is 40% salt. How many ounces of each solution should she use?

Answer 1

Given:

• Solution A is 30% salt, and solution B is 75% salt.
• The final solution has 180 ounces of a mixture that is 40% salt.

Required:

How many ounces of each solution should she use?

Step-by-step explanation:

Let us assume that,

• x be the number of ounces of solution A.
• y be the number of ounces of solution B.

Now the equation can be written as,

`x + y = 180`

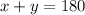
and

`x * 30\% + y * 75\% = 180 * 40\% \\ 30x + 75y = 7200`

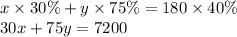
Let's solve them as,

`30x + 75y - (30x + 30y) = 7200 - 5400\\ 45y = 7020 \\ y = ( 1800)/(45) \\ y = 40`

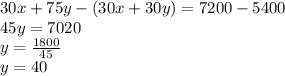
The value of x will be,

`x = 180 - 40 \\ x = 140`

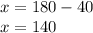
Final answer:

So, the scientist should use 140 ounces of solution A and 40 ounces of solution B to obtain 180 ounces of a mixture that is 40% salt.