Final answer:
The general solution of the differential equation
 is
is
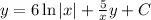 , where
, where
 is the constant of integration. The corresponding particular solution, given the initial condition
is the constant of integration. The corresponding particular solution, given the initial condition
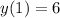 , is
, is
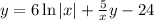 .
.
Step-by-step explanation:
To find the general solution of the given differential equation
 , we can use the method of separation of variables. Rearranging the equation, we have:
, we can use the method of separation of variables. Rearranging the equation, we have:

Multiplying both sides of the equation by
 , we get:
, we get:

This is a linear first-order differential equation. We can separate the variables by moving all terms involving
 to one side and all terms involving
to one side and all terms involving
 to the other side:
to the other side:
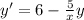
Next, we can divide both sides of the equation by
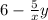 to isolate
to isolate
 :
:
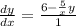
Now, we can integrate both sides of the equation with respect to

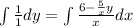
Simplifying the integrals, we have:
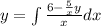
Integrating the right side of the equation, we get:

Using the power rule of integration, we can evaluate the integral:
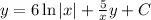
where
 is the constant of integration.
is the constant of integration.
This is the general solution of the differential equation
 .
.
To find the corresponding particular solution, we can use the given initial condition
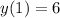 . Substituting
. Substituting
 and
and
 into the general solution, we have:
into the general solution, we have:

Simplifying the equation, we get:
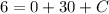
Solving for
 , we find:
, we find:

Substituting
 back into the general solution, we obtain the particular solution:
back into the general solution, we obtain the particular solution:
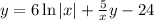
This is the general solution and the corresponding particular solution of the given differential equation.