Question

!50 POINTS! (1 SIMPLE GEOMETRY QUESTION)

QUESTION BELOW
|
|
\/

Answer 1

c) 40.3

`\hrulefill`

Explanation:

According to the Alternate Exterior Angles Theorem, when two parallel lines are intersected by a transversal, the angles that are exterior to the parallel lines and on the alternate sides of the transversal are congruent.

Therefore, if lines r and s are parallel, then a° = b°.

To find the value of x that proves line r is parallel to line s, solve a° = b° for x.

`\begin{aligned}a^(\circ)&=b^(\circ)\\\\3x+17&=138\\\\3x+17-17&=138-17\\\\3x&=121\\\\(3x)/(3)&=(121)/(3)\\\\x&=40.33333....\\\\x&=40.3\; \sf (nearest\;tenth)\end{aligned}`

Therefore, the value x that proves line r is parallel to line s is:

`\Large\boxed{x=40.3}`

Answer 2

x= 40.33

Explanation:

In geometry, alternate exterior angles are a pair of angles that are on the outer side of two parallel lines but on opposite sides of the transversal. In other words, they are the angles that are not on the same line as the parallel lines.

The alternate exterior angles are always equal in measure. This is because when a transversal intersects two parallel lines, it creates two pairs of alternate exterior angles, and each pair of angles is supplementary to each other (meaning that their measures add up to 180 degrees).

In this case:

a° = b°

Since,, the alternate exterior angles are always equal in measure.

3x+17 = 138

subtracting 17 on both sides

3x + 17-17 = 138-17

3x = 121

dividing both sides by 3.

`(3x)/(3) = (121)/(3)`

`\sf x \approx 40.33`

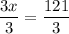
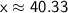
The value of x is 40.33 which proves that r is parallel to s.