Answer:
Question 47: Option C:
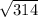
Question 48: Option A: 46 feet
Question 49: Option D: (-2, 3)
Explanation:
We can use the distance formula to find the length of ST, which is given by:
d = sqrt[(x2 - x1)² + (y2 - y1)²]
where (x1, y1) is the coordinate of point S and (x2, y2) is the coordinate of point T.
Substituting the given values, we get:
d = sqrt[(2 - (-3))² + (-8 - 9)²]
= sqrt[(2 + 3)² + (-17)²]
= sqrt[5² + 17²]
= sqrt[25 + 289]
= sqrt[314]
Therefore, the length of ST is sqrt(314), which is option C. (Question 47)
The length of the railing needed for the curved section of the balcony is the arc length of the circle subtended by the central angle of 70 degrees.
The formula to find the length of an arc of a circle of radius "r" subtended by a central angle of "θ" degrees is given by:
Arc length = (θ/360) * 2πr
Substituting the given values, we get:
Arc length = (70/360) * 2π(38)
= (7/36) * 2π(38)
= (7/18)π(38)
= (133/9)π
≈ 46.68 feet
Therefore, the closest option to the length of the railing needed for the curved section of the balcony is A) 46 feet. (Question 48)
Since the diagonals of a rectangle intersect at their midpoint, we can use this information to find the coordinates of the opposite vertex of the rectangle.
Let's denote the midpoint of the diagonals (2, 1) as M. We can find the coordinates of the opposite vertex of the rectangle as follows:
1) Find the vector from M to (-4, 5):
(-4, 5) - (2, 1) = (-6, 4)
2) Since the opposite diagonal of the rectangle is perpendicular to the diagonal that passes through M, we can find the vector perpendicular to (-6, 4) by swapping the coordinates and negating one of them:
(-4, -6) = (-4, -(2*2))
3) The opposite vertex of the rectangle is located at the endpoint of the vector obtained in step 1, added to the vector obtained in step 2:
(2, 1) + (-4, -6) = (-2, -5)
Now we can check which of the given answer choices has (-2, -5) as one of its vertices:
- A. (-10, 9): This cannot be a vertex of the rectangle since it is not opposite to (-4, 5) and does not have (-2, 1) as its midpoint.
- B. (3, -1): This cannot be a vertex of the rectangle since it does not have (-2, 1) as its midpoint.
- C. (8, -3): This cannot be a vertex of the rectangle since it is not opposite to (-4, 5) and does not have (-2, 1) as its midpoint.
D. (-2, 3): This could be a vertex of the rectangle since it is opposite to (-4, 5) and has (-2, 1) as its midpoint.
Therefore, the answer is D. (-2, 3). (Question 49)
---------------------
Subject: Geometry - MATHEMATICS 10