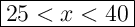Question

HEY! GIVING A TON OF POINTS TO A TON OF PEOPLE, YOU JUS NEED TO BE GOOD AT SIMPLE GEOMETRY. (Im gonna be postin a ton of simple geometry questions all for 50 points to whoever can complete them all and get the correct answers only)

SO IF YOUR GOOD AT GEOMETRY... PROOVE IT! By just answering this one geo questions below:

Answer 1

a) 25 < x < 40

`\hrulefill`

Explanation:

According to the Triangle Inequality Theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Therefore, if a, b, and c are the lengths of the sides of a triangle, then:

• a + b > c
• a + c > b
• b + c > a

Given the sides of the triangle are 15 inches, 40 inches and "x" inches, using the Triangle Inequality Theorem we can write the following inequalities:

`\textcircled{1}\quad 15 + 40 > x`

`\textcircled{2}\quad 15 + x > 40`

`\textcircled{3}\quad40 + x > 15`

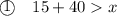
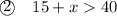
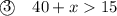
Solve each inequality for x:

`\begin{aligned}\textcircled{1}\quad 55 & > x \\x & < 55\end{aligned}`

`\begin{aligned}\textcircled{2}\quad 15 + x & > 40\\x& > 40-15\\x& > 25\end{aligned}`

`\begin{aligned}\textcircled{3}\quad40 + x& > 15\\x& > 15-40\\x& > -25\end{aligned}`

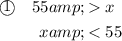
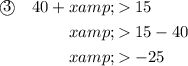
The first inequality tells us that x should be less than 55 inches.

The second inequality tells us that x should be greater than 25 inches.

The third inequality tells us that x should be greater than -25 inches. Therefore, x is greater than zero, since length cannot be negative.

To find the possible values of x that satisfy all three inequalities, we need to consider the intersection of the solutions for each individual inequality.

Therefore, the range of possible lengths for the third side, x, of the triangle is:

`\Large\boxed{25 < x < 40}`