Question

One side of a square was shortened by 3 inches and the other side was lengthened by 5 inches. The area of the new square is 55 inches greater than half the area of the original square. Find the length of a side of the original square

Answer 1

10

Explanation:

Let's say the side of a square is
`s`

Then the area of the original square would be
`s^2`

After modification, the sides of the new quadrilateral would be
`s-3` and
`s+5`

Meaning that the area of the new quad. which is equal to
`(s^2)/(2) +55` would also be equal to
`(s-3)(s+5)`

Using the FOIL method, we get

`(s-3)(s+5)\\s^2+5s-3s-15\\s^2+2s-15`

That means that
`(s^2)/(2) +55`
`=s^2+2s-15`

Multiplying both sides by two gets us to
`s^2+110=2s^2+4s-30`

Subtract both sides by
`s^2` --->
`110=s^2+4s-30`

Subtract
`110` from both sides --->
`s^2+4s-140=0`

Factor --->
`(s+14)(s-10)`

Since the side of a square cannot be negative, that eliminates the option of
`s=-14` and leaves us with an answer of
`s=10`.

If doubts still remain, we can simply check this by plugging in the number 10:

Original area=
`10^2` or
`100`

`10-3=7, 10+5=15`

`15*7=105`

`(1)/(2)` of the original area is
`50\\`

`50+55=105`

Meaning that
`10` is the correct answer.

Answer 2

10 inches

Explanation:

Let x be the length of one side of the original square.

According to the question:

One side is shortened by 3 inches can be expressed as (x-3)

Another side was lengthened by 5 inches can be expressed as (x+5)

We know that:

`\sf \textsf{The area of the original square }(A_O)=Length*Length = x* x=x^2.`

`\sf \textsf{The area of the New square }(A_N)=Length*Length =(x-3)(x+5).`

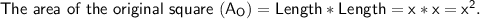
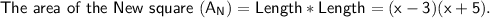
Again, we know that

The area of the new square is 55 inches greater than half the area of the original square.

This can be expressed as:

`\sf A_N - 55 = (A_O)/(2)`

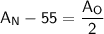
Substituting value

`\sf (x-3)(x+5) -55 =(x^2)/(2)`

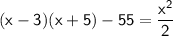
Expanding the left side of the equation, we get

`\sf x(x+5)-3(x+5) -55 =(x^2)/(2)`

`\sf x^2+5x-3x-15 -55 =(x^2)/(2)`

`\sf x^2+2x - 70 = (x^2)/(2)`

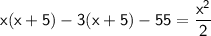
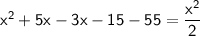
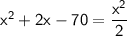
doing Criss cross multiplication

`\sf 2x^2+4x-140 = x^2`

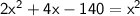
keeping x^2 in left side

`\sf 2x^2 - x^2 +4x -140 =0`

`\sf x^2 +4x -140 = 0`

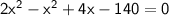
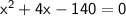
We can solve for x using the quadratic formula:

`\sf x = (-b\pm √(b^2 - 4ac))/( 2a)`

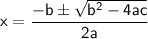
Comparing above equation with
`\sf \underline{ax^2 +bx+ c}`

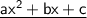
In this case, a = 1, b = 4, and c = -140.

Substituting these values into the quadratic formula, we get:

`\sf x = (-4 \pm √(4^2 - 4 * 1 * -140))/( 2 * 1)`

`\sf x = (-4 \pm √(576))/(2)`

`\sf x = (-4 \pm 24)/(2)`

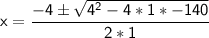
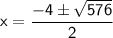
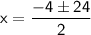
Taking positive

`\sf x = (-4 + 24)/(2)`

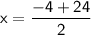
x = 10

Taking Negative

`\sf x = (-4 - 24)/(2)`

x = -14

Since length of sqaure is always positive.

Therefore, the length of a side of the original square is 10 inches.