Question

The image of a composite figure is shown.
What is the area of the figure?

Answer 1

The answer will end up being 64.2

Explanation:

The simple way to explain this is by moving the triangle on the left of the red dotted line onto the right side. After this you can add 4 and 6.7 to get 10.7 and multiply that by 6 to get the answer of 64.2.

Answer 2

64.2 ft²

Explanation:

The composite figure is the mixture of the Traingle and Trapezoid.

Left side having thre side is triangle and remaining one is Trapezoid.

Now,

The area of a triangle is equal to half the product of its base and its height.

The formula is:

`\boxed{\textsf{Area of triangle }=\sf (1)/(2)bh}`

where b is the base and h is the height of the triangle.

In this case:

b= 4ft

h = 6ft

Substituting value in formula, we get

`\textsf{Area of triangle= }\sf (1)/(2)4*6=12 ft^2`

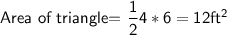
Again

The area of a trapezoid is equal to half the sum of its bases times its height.

The formula is:

`\boxed{\textsf{Area of trapezoid = }\sf (1)/(2)(a + b)h}`

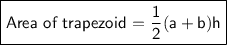
where a and b are the bases of the trapezoid and h is its height.

In this case:

a=6.7 ft

b = 10.7 ft

h=6 ft

Substituting value

`\textsf{Area of trapezoid }=\sf (1)/(2)(6.7+10.7)6 = 52.2 ft^2`

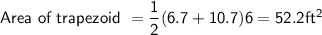
Now

Total Area = Area of triangle+ Area of trapezoid

Total Area= 12 + 52.2

Total Area = 64.2 ft²

Therefore the area of the composite figure is 64.2 ft².