Question

If the radius of circle A is 7 units, and if ADGH and ADFE are isosceles right* triangles with ED = DF = 2 and DH = DG = 9, approximate the area of the shaded region. (Use π = 3.14159). Round to the nearest hundredth. *Image not to scale. Answer ASAP

Answer 1

111.44 units

Explanation:

Since triangles DGH and DFE are both right isosceles, that means that we can apply the formula A=s^2/2 to find the area.

DGH: DG=DH=s=9

Thus: A=(9^2)/2

A=81/2

A=40.5

DFE: ED=DF=s=2

Thus: A=(2^2)/2

A=4/2

A=2

40.5+2=42.5 (Area of both triangles added together)

Now, to find the area of the circle, we use the formula A=πr^2.

Since we know that r=7, we can plug it into the formula to get

A=π(7^2)

A=3.14159*49

A=153.93791

Now, to find the area of the shaded region, we subtract the area of the circle by the area of the triangles combined.

A=153.93791-42.5

A=111.43791

After rounding, it turns into A=111.44

Answer 2

Area of the shaded region in the circle is 68.94 square units.

To find the area of the shaded region in the diagram, we need to follow these steps:

1. Calculate the area of the circle.

2. Calculate the area of the four triangles within the circle.

3. Subtract the total area of the triangles from the area of the circle.

Given:

- The radius of circle A is r = 7 units.

- ED = DF = 2 units and DH = DG = 9 units, which are the legs of the isosceles right triangles ADGH and ADFE .

For the isosceles right triangles, we can use the legs to find the area. Since they are isosceles right triangles, the area of each triangle is
`\( (1)/(2) * \text{leg} * \text{leg} \).`

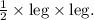
Steps:

Area of the Circle:

`\[ \text{Area}_{\text{circle}} = \pi r^2 \]\[ \text{Area}_{\text{circle}} = 3.14159 * 7^2 \]`

Area of One Small Triangle (ADFE):

`\[ \text{Area}_{\text{small triangle}} = (1)/(2) * ED * DF \]\[ \text{Area}_{\text{small triangle}} = (1)/(2) * 2 * 2 \]`

Area of One Large Triangle (ADGH):

`\[ \text{Area}_{\text{large triangle}} = (1)/(2) * DH * DG \]\[ \text{Area}_{\text{large triangle}} = (1)/(2) * 9 * 9 \]`

Total Area of Triangles:

`\[ \text{Total area}_{\text{triangles}} = 2 * \text{Area}_{\text{small triangle}} + 2 * \text{Area}_{\text{large triangle}} \]`

Area of Shaded Region:

`\[ \text{Area}_{\text{shaded}} = \text{Area}_{\text{circle}} - \text{Total area}_{\text{triangles}} \]`

Let's perform the calculations.

The area of the shaded region in the circle is approximately 68.94 square units when rounded to the nearest hundredth.