Question

If f(x)= and g(x)=, which of the following is the domain of the function f + g?

O The set of all real numbers
O The set of all real numbers except 1
O The set of all real numbers except 0 and 1
O The set of all positive real numbers

Answer 1

Answer: Choice C

The set of all real numbers except 0 and 1

Reason:

We have these defined functions

`f(\text{x}) = \frac{\text{x}}{1-\text{x}}\\\\g(\text{x}) = \frac{1}{\text{x}}\\\\`

Which would mean

`f(\text{x})+g(\text{x}) = \frac{\text{x}}{1-\text{x}}+\frac{1}{\text{x}}\\\\`

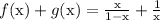
That can be simplified, but it's not really needed here.

The first denominator 1-x means x = 1 is not allowed, or else we'll have a division by zero error.

Similarly, the second denominator x will have x = 0 not be allowed in the domain.

Any other real number will work in the domain.

The graph of f(x)+g(x) involves vertical asymptotes at x = 0 and x = 1.

Use a tool like Desmos or GeoGebra to confirm this claim.