Question

Please provide the measurements labelled in the image. Please include all measurements.

Answer 1

Check the picture below.

now, we're making the assumption that the triangle above is an isosceles, so let's find "x" and "y" to get the area of the triangle and thus add it to the area of the rectangle and have the whole area of the shape.

`\textit{Law of Sines} \\\\ \cfrac{a}{\sin(\measuredangle A)}=\cfrac{b}{\sin(\measuredangle B)}=\cfrac{c}{\sin(\measuredangle C)} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{y}{\sin(90^o)}=\cfrac{17.5}{\sin(62.8^o)}\implies y\sin(62.8^o)=17.5\sin(90^o) \\\\\\ y=\cfrac{17.5\sin(90^o)}{\sin(62.8^o)}\implies \boxed{y\approx 19.68} \\\\[-0.35em] ~\dotfill`

`\cfrac{x}{\sin(27.2^o)}=\cfrac{17.5}{\sin(62.8^o)}\implies x\sin(62.8^o)=17.5\sin(27.2^o) \\\\\\ x=\cfrac{17.5\sin(27.2^o)}{\sin(62.8^o)}\implies \boxed{x\approx 8.99}`

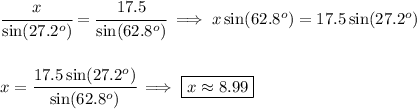
now, I take it the so-called "area sine formula" is just the same as getting the area using "x" since we got "x" using the law of sines, so let me nevermind that part and get the area of the triangle using "x".

`\stackrel{ \textit{\LARGE Areas} }{\stackrel{\textit{triangle}}{\cfrac{1}{2}(\underset{b}{35})(\underset{h}{x})}~~ + ~~\stackrel{rectangle}{(10)(35)}}\implies \cfrac{1}{2}(\underset{b}{35})\underset{h}{\left(\cfrac{17.5\sin(27.2^o)}{\sin(62.8^o)}\right)}~~ + ~~(10)(35) \\\\\\ ~\hfill~\approx\text{\LARGE 507.39}~ft^2~\hfill~`

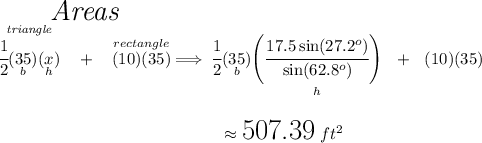
Make sure your calculator is in Degree mode.