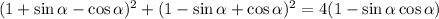Answer:
See the below explanation for proof.
Explanation:
Given trigonometric equation:
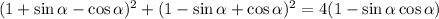
To prove the equation, manipulate the left side of the equation until it equals the right side.
Expand the first set of parentheses on the LHS of the equation by using the identity:
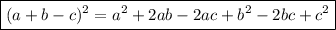
Therefore:
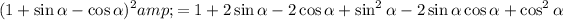
Simplify by using the trigonometric identity sin²x + cos²x = 1:
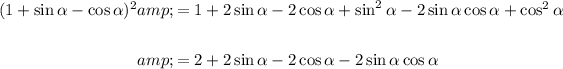
Expand the second set of parentheses on the LHS of the equation by using the identity:
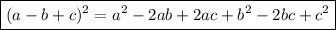
Therefore:
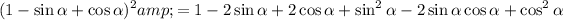
Simplify by using the trigonometric identity sin²x + cos²x = 1:
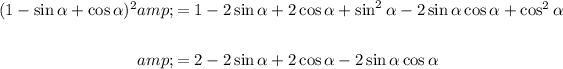
Therefore:
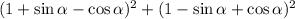
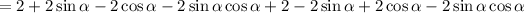
Simplify by combining like terms:
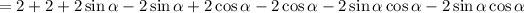

Factor out the common term 4:
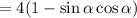
Therefore, we have proved that the left side of the equation equals the right side: